Với giá trị nào của m thì hàm số đồng biến trên khoảng ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Điều kiện tanx ≠ m
Điều kiện cần để hàm số đồng biến trên (0; π/4) là m ∉ (0;1)
+) đạo hàm:
y ' = ( tan 2 x + 1 ) ( 2 - m ) ( tan x - m ) 2 = 2 - m cos 2 x . ( tan x - m ) 2
+) Ta thấy:
1 cos 2 x . ( tan x - m ) 2 > 0 ; ∀ m ∉ ( 0 ; 1 )
+) Để hàm số đồng biến trên (0; π/4)
⇔ y ' > 0 m ∉ ( 0 ; 1 ) ⇔ - m + 2 > 0 m ≤ 0 ; m ≥ 1 ⇔ m ≤ 0 h o ặ c 1 ≤ m < 2
Chọn D.

Đáp án B
Đặt ![]() .
.
Với 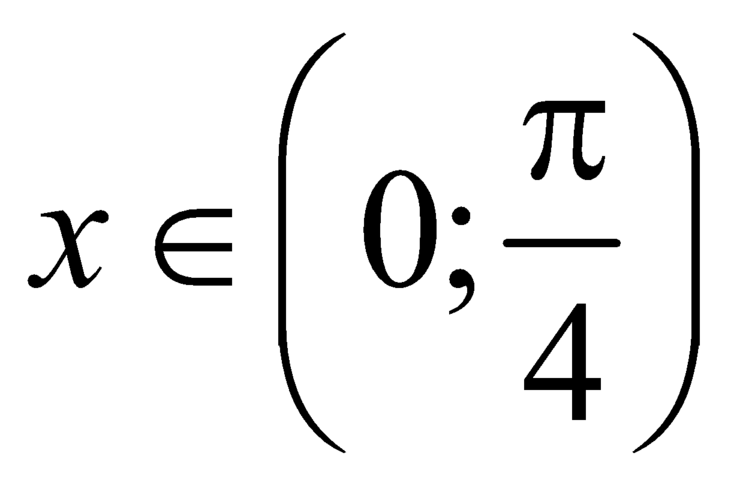 thì
thì ![]() , hàm số trở thành
, hàm số trở thành ![]() .
.
Đạo hàm 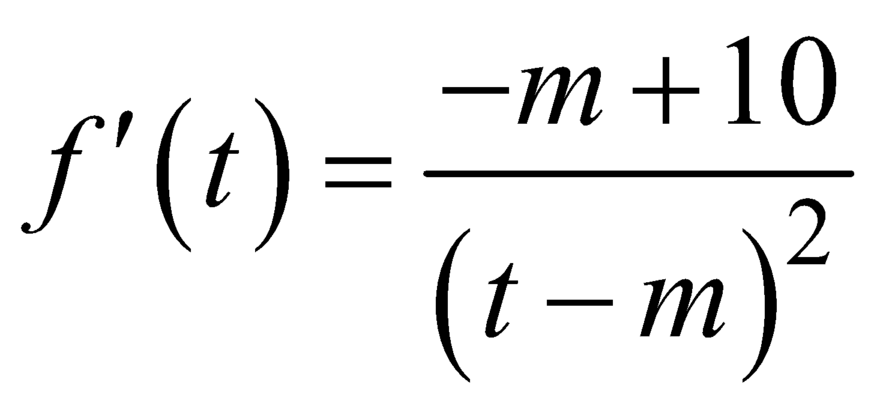 .
.
Hàm số đồng biến trên ![]() khi
khi
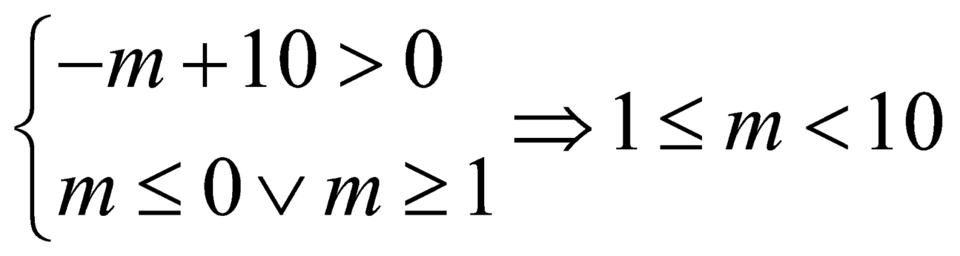 .
.
Vậy có 9 giá trị nguyên của m

Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
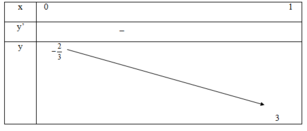
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)

Đáp án D
Hàm số đồng biến trên khoảng (2;+∞)
⇔ y’ ≥ 0 ∀ x ϵ D (2;+∞)
Ta có: (-m; +∞) = D (2;+∞)
ð m ≥ -2
Ta có: y’ = m 2 − 3 ( x + m ) 2
ð y’ ≥ 0 ⇔ m ≥ 3 hoặc m ≤ - 3
Vậy tập giá trị m thỏa mãn đề bài là: m ≥ 3 hoặc -2 ≤ m ≤ - 3




Đáp án A
Đặt t = tanx, ta tìm m để hàm số