Trong mặt phẳng Oxy cho v → 1 ; 2 , điểm M(2;5). Tìm tọa độ ảnh của điểm M qua phép tịnh tiến v →
A. (1;6)
B. (3;7)
C. (4;7)
D. (3;1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
EW
0
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2020
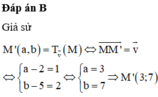
14.
\(\overrightarrow{AB}=\left(-3;10\right)\Rightarrow\) đường thẳng AB nhận \(\left(10;3\right)\) là 1 vtpt
Phương trình AB:
\(10\left(x-3\right)+3\left(y+4\right)=0\Leftrightarrow10x+3y-18=0\)
16.
Do d song song denta nên d nhận \(\left(3;-2\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-2\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y-4=0\)
17. Cho d vuông góc denta nên d nhận \(\left(1;-1\right)\) là 1vtpt
Phương trình d:
\(1\left(x-4\right)-1\left(y+1\right)=0\Leftrightarrow x-y-5=0\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
14.
\(\overrightarrow{AB}=\left(-3;10\right)\) nên pt tham số của AB là: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+10t\end{matrix}\right.\)
15.
Do d song song delta nên d nhận \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=2t\\y=-4-t\end{matrix}\right.\)
18.
d có vtcp là (2;3) nên d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x+1\right)-2\left(y-0\right)=0\Leftrightarrow3x-2y+3=0\)
19.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-4\right)=0\Leftrightarrow4x+3y-4=0\)
20 tháng 1 2023
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
CM
6 tháng 2 2019
Ta có: u → = ( − 1 ) 2 + x 2 = 1 + x 2 ; v → = 2 2 + 4 2 = 20
Để hai vecto này có độ dài bằng nhau khi và chỉ khi: 1 + x 2 = 20
⇔ 1 + x 2 = 20 ⇔ x 2 = 19 ⇔ x = ± 19
Chọn D.
CM
25 tháng 7 2017
Đáp án B
Ta có: T v → ( M ) = M ' = M M ' → = v → ⇔ x M ' - 1 = 3 y M ' + 2 = - 2 ⇔ x M ' = 4 y M ' = - 4 . Vậy M'(4;-4)