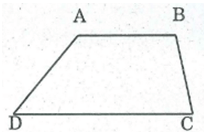
cho hình thang cân ABCD (AB//CD) có góc A =3 góc D . tính các góc của hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)

Ta có: \(\widehat{A}+\widehat{D}=180^o\)
Mà \(\widehat{A}=3\widehat{D}\)
\(\Rightarrow\widehat{A}=135^o;\widehat{D}=45^o\)
Ta có:\(\widehat{A}=\widehat{B}\);\(\widehat{C}=\widehat{D}\)

Vì ABCD là htc nên \(\widehat{A}=2\widehat{C}=2\widehat{D}\)
Mà AB//CD nên \(\widehat{A}+\widehat{D}=180^0\Rightarrow3\widehat{D}=180^0\Rightarrow\widehat{D}=60^0\Rightarrow\widehat{A}=120^0\)
Vì ABCD là htc nên \(\widehat{A}=\widehat{B}=120^0;\widehat{D}=\widehat{C}=60^0\)

Do AB // CD ( GT )
⇒^A+^C=180o
⇒2^C+^C=180o
⇒3^C=180o
⇒^C=60o
⇒ ^A = 60o * 2 = 120o
Do ABCD là hình thang cân
⇒ ^C = ^D
Mà ^C = 60o
⇒ ^D = 60o
AB // CD ⇒ ^D + ^B = 180o
⇒ˆB=180o − 60o = 120o
Vậy ^A = ^B = 120o ; ^C= ^D = 60o
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB : Cạnh chung
^DAB=^CBA (Tính chất của hình thang cân)
AC = BD ( Tính chất của hình thang cân)
⇒ ΔADB = ΔBCA ( c−g−c)
⇒ ^CAB = ^DBA (2 góc tương ứng)
⇒ ^OAB = ^OBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh

Vì ABCD là hình thang cân
=> \(\hept{\begin{cases}\widehat{C}=\widehat{D}\\\widehat{B}=\widehat{A}\end{cases}}\)
Mà \(\widehat{A}=2\widehat{C}\)
=> \(\widehat{A}=2\widehat{D}\)
Vì AB // CD
=> \(\widehat{A}+\widehat{D}=180^o\)
Thay \(\widehat{A}=2\widehat{D}\)
=> \(3\widehat{D}=180^o\)
=> \(\widehat{D}=180^o:3=60^o\)
và \(\widehat{A}=2.\widehat{D}=2.60^o=120^o\)
Vì \(\widehat{C}=\widehat{D}\Rightarrow\widehat{C}=60^o\)
Vì \(\widehat{B}=\widehat{A}\Rightarrow\widehat{B}=120^o\)
Vậy \(\widehat{A}=120^o;\widehat{B}=120^o;\widehat{C}=60^o;\widehat{D}=60^o\)

BÀI 2; Cho hình cân ABCD ( AB // CD ) ; góc A = 120 độ. Tính các góc còn lại của hình thang.
Giải:
Xét hình thang cân ABCD ta có:
góc BAD + góc ADC = 180 độ ( 2 góc trong cùng phía bù nhau do AB//CD)
=> 120 độ + góc ADC = 180 độ
=> góc ADC = 60 dộ
Vì tiws giác ABCD là hình thang cân
=> góc BAD = góc ABC = 120 độ
=> góc ADC = góc BCD = 60 độ

Ta có A ^ + D ^ = 180 0 , A ^ = 2 C ^ = 2 D ^
Suy ra C ^ = D ^ = 60 0 , A ^ = B ^ = 120 0

Tương tự bài 1A. Ta có: C ^ = D ^ = 45 0 , A ^ = B ^ = 135 0

a =135 độ
b=135 độ
c=45 độ
d=45 độ