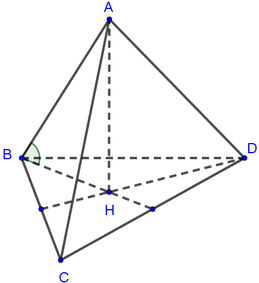
Cho tứ diện đều ABCD. Tính tang của góc giữa AB và (BCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

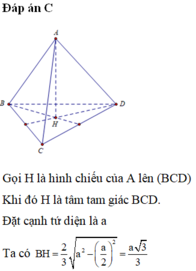
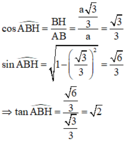

Đáp án C
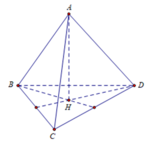
Gọi H là hình chiếu của A lên (BCD)
Khi đó H là tâm tam giác BCD.
Đặt cạnh tứ diện là a
Ta có B H = 2 3 a 2 − a 2 2 = a 3 3
cos A B H ^ = B H A B = a 3 3 a = 3 3 sin A B H ^ = 1 − 3 3 2 = 6 3 ⇒ tan A B H ^ = 6 3 3 3 = 2

Đáp án C
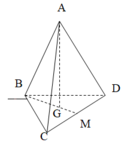
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
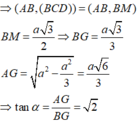

Đáp án C
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
⇒ ( A B , ( B C D ) ) = ( A B , B M ) B M = a 3 2 ⇒ B G = a 3 3 A G = a 2 − a 2 3 = a 6 3 ⇒ tan α = A G B G = 2
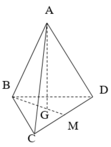

Đáp án C
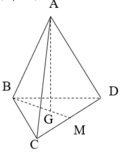
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
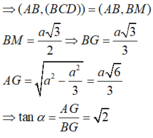

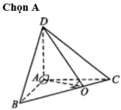
Gọi O là hình chiếu vuông góc của A lên cạnh BC. Khi đó góc giữa hai mặt phẳng (ABC) và (BCD) là
![]()