Nếu log7 x = log7 ab2 – log7 a3b (a, b > 0) thì x nhận giá trị là A. a2b. B. ab2. C. a2b2. D. a–2b....
Đọc tiếp
Nếu log7 x = log7 ab2 – log7 a3b (a, b > 0) thì x nhận giá trị là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 5 2017
Đáp án C
Ta có: log 25 56 = 1 2 log 5 56 = 1 2 log 5 2 3 .7 = 1 2 3. log 5 2 + log 5 7 .
Mà log 5 100 = 2 log 5 10 = 2 1 + log 5 2 = b ⇒ log 5 2 = b 2 − 1 và log 7. log 5 10 = log 5 7 = a b 2 .
Vậy log 25 56 = 1 2 3. b 2 − 1 + a b 2 = a b + 3 b − 6 4 .
PT
1
CM
11 tháng 7 2019
Chọn C.
Điều kiện: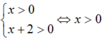 
Đặt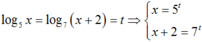 
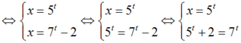
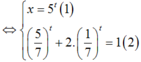
Nhận thấy t = 1 là một nghiệm của phương trình (2).
Xét hàm số 
trên R
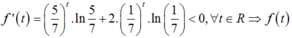nghịch biến trên R và f(t) = f(1) khi và chỉ khi t = 1.
Thay t = 1 vào (1) suy ra x = 5.
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2021
\(log_7\left(4x^2-4x+1\right)-log_72x+4x^2+1=6x\)
\(\Leftrightarrow log_7\left(4x^2-4x+1\right)+4x^2-4x+1=log_72x+2x\)
\(\Rightarrow4x^2-4x+1=2x\)
\(\Rightarrow...\)
5 tháng 10 2021
log7(4x2−4x+1)−log72x+4x2+1=6xlog7(4x2−4x+1)−log72x+4x2+1=6x
=log7(4x2−4x+1)+4x2−4x+1=log72x+2x⇔log7(4x2−4x+1)+4x2−4x+1=log72x+2x
=4x2−4x+1=2x⇒4x2−4x+1=2x
= 2x
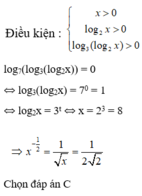
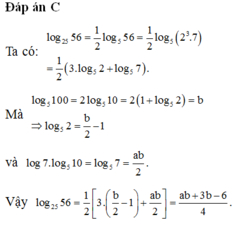
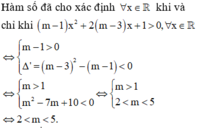
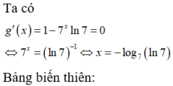
Đáp án D.
log 7 x = log 7 a b 2 – log 7 a 3 b = log 7 a b 2 a 3 b = log 7 b a - 2
Do đó x = a–2b.