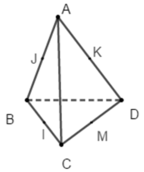
Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường th...

PT

Pham Trong Bach

20 tháng 8 2019

Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 8 2019

Đúng(0)

GM

Gấu mập

15 tháng 7 2021

Cho tứ giác ABCD có góc A=góc B=90 độ a)Cm AD//BC b)Cho D=3C.Tính C,D c)Cho D-C=30 độ.Tính C,D

#Hỏi cộng đồng OLM #Toán lớp 8

1

KN

Khuất Ngọc Nam

15 tháng 7 2021

a) Có AD ⊥ AB( góc A vuông)
BC ⊥ AB( góc B vuông)
=> AD // BC
b) Có tứ giác ABCD= 360 độ
mà A = B= 90 độ
=> C + D= ABCD - A - B
= 360 độ - 90 độ - 90 độ
= 180 độ
Có D = 3C và C + D = 180 độ
=> C = 45 độ
=> D = 135 độ
c) Có ABCD= 360 độ
A = B= 90 độ
=> C + D= 180 độ
=> D =180 độ - C
+) D - C = 30 độ
<=> 180 độ - C - C = 30 độ
<=> 2C= 150 độ
<=> C = 75 độ
=> D = 105 độ
Vậy a) AD // BC
b) C = 45 độ
D = 135 độ
c) C = 75 độ
D = 105 độ

Đúng(1)

BH

baek huyn

29 tháng 11 2018 - olm

Cho hình thang vuông ABCD A=D=90 độ , AB=AD=3cm , CD=6cm

a,tính số đo các góc B, góc C và độ dìa canh bên BC của hình thang

b,gọi BH là đường cao của hình thnag ABCD( H thuộc CD) .Tứ giác ABCH là hình gì ? vì sao ?

c, tính diện tích tứ giác ABCH?

#Hỏi cộng đồng OLM #Toán lớp 8

1

NH

Nguyễn Hoàng Đăng

29 tháng 11 2018

Chắc Biết

Đúng(0)

PT

Pham Trong Bach

9 tháng 10 2019

Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó A. h = a 13 2 B. h = a 13 4 C. ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

9 tháng 10 2019

Đúng(0)

PT

Pham Trong Bach

7 tháng 5 2019

Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó. A. h = a ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

7 tháng 5 2019

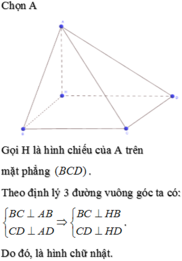
Chọn B

Gọi I là trung điểm AB, J là trung điểm CD

Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD

=> IJ = a

Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD

=> O nằm trên IJ => Ta cần tính OA

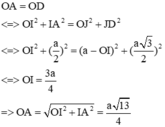
Ta có:

Đúng(0)

TS

Trần Sơn

7 tháng 9 2017 - olm

Cho tứ giác abcd có góc a=góc c=90 độ gọi b',d' lần lượt là hình chiếu của b,d trên đường chéo ac. chứng minh rằng ab'=cd'

#Hỏi cộng đồng OLM #Toán lớp 9

0

OB

Oo Bản tình ca ác quỷ oO

17 tháng 8 2017 - olm

1/ cho tứ giác ABCD có góc B = góc D = 90 độ.

a) chứng minh A,B,C,D cùng thuộc 1 đường tròn.

b) so sánh AC và BD, nếu AC = BD thì tứ giác ABCD là hình gì?

c)cho góc BAC = 30 độ, DAC = 40 độ. hãy so sánh khoảng cách từ O đến BC,CD.

giúp mjk nha m.n!! thks nhìu ^^

#Hỏi cộng đồng OLM #Toán lớp 9

1

HH

Huy Hoang

17 tháng 7 2020

A B C D I

a. Gọi M là trung điểm của AC

Tam giác ABC vuông tại B có BM là đường trung tuyến nên:

\(BM=\left(\frac{1}{2}\right).AC\)(tính chất tam giác vuông)

Tam giác ACD vuông tại D có DM là đường trung tuyến nên:

\(DM=\left(\frac{1}{2}\right).AC\) (tính chất tam giác vuông)

Suy ra: MA = MB = MC = MD

Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng \(\left(\frac{1}{2}\right).AC\)

b. Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC

AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật

Đúng(1)

HK

hoàng khánh linh

20 tháng 6 2018 - olm

Bài 1: Tính số đo các góc C và D của tứ giác ABCD biết góc A=120 độ, góc B=90 độ, góc C=2.góc DBài 2: Cho tứ gics ABCD có góc A=góc B và BC=AD. Cm:a) Tứ gác DAB= tứ giác CBA, từ đó \(\Rightarrow\)BD=ACb) Góc ADC=góc BCDc) AB//CDBài 3: Cho tứ giác ABCD và 1 điểm M thuộc miền trong của tứ giác. Cm: MA+MB+MC+MD \(\ge\)AB+CDCác bn trả lời giúp mik...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 8

0

PT

Pham Trong Bach

3 tháng 1 2019

Cho tứ diện ABCD có BC=a, C D = a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

3 tháng 1 2019

Đúng(0)

PT

Pham Trong Bach

19 tháng 8 2019

Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:

A. trung điểm J của AB

B. trung điểm I của BC

C. trung điểm K của AD

D. trung điểm M của CD

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

19 tháng 8 2019

CD ⊥ (ABC) vì CD ⊥ AB và CD ⊥ BC

AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD

Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C

Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C

Phương án C đúng vì tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B và D

Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D.

Đáp án C

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP