Cho đồ thị . Tất cả giá trị của tham số m để cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toi mới làm được câu 2 thoi à :( Mấy câu còn lại để rảnh nghĩ thử coi sao
\(PTHDGD:\dfrac{x+1}{x-1}=2x+m\Leftrightarrow x+1=\left(2x+m\right)\left(x-1\right)\)
\(\Leftrightarrow x+1=2x^2-2x+mx-m\Leftrightarrow2x^2+\left(m-3\right)x-m-1=0\)
De ton tai 2 diem phan biet \(\Leftrightarrow\Delta>0\Leftrightarrow\left(m-3\right)^2+8m+8>0\Leftrightarrow m^2+2m+17>0\Leftrightarrow\left(m+1\right)^2+16>0\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{3-m}{2}\\x_1x_2=\dfrac{-m-1}{2}\end{matrix}\right.\)
Vi 2 tiep tuyen tai 2 diem x1, x2 song song voi nhau
\(\Rightarrow f'\left(x_1\right)=f'\left(x_2\right)\)
\(f'\left(x\right)=\dfrac{x-1-x-1}{\left(x-1\right)^2}=-\dfrac{2}{\left(x-1\right)^2}\)
\(\Rightarrow\dfrac{1}{\left(x_1-1\right)^2}=\dfrac{1}{\left(x_2-1\right)^2}\Leftrightarrow x_1^2-2x_1+1=x_2^2-2x_2+1\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)-2\left(x_1-x_2\right)=0\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=x_2\left(loai\right)\\x_1+x_2=2\end{matrix}\right.\Leftrightarrow\dfrac{3-m}{2}=2\Leftrightarrow m=-1\)

Chọn D.
Phương trình hoành độ giao điểm (C) và d là :
![]()
![]()
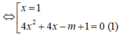
Để (C) cắt d tại một điểm ⇔ Phương trình (1) vô nghiệm hay phương trình (1) có nghiệm kép bằng 1
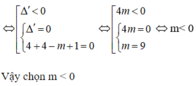

1/ \(y=x^3+3x^2+mx+m-2\)
\(y'=3x^2+6x+m\)
Chia đa thức \(y\) cho \(y'\) được phần dư là \(\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
\(\Rightarrow\)Phương trình đường thẳng \(d\) đi qua 2 cực trị có dạng:
\(y=\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
Gọi A là giao điểm của \(d\) với \(Ox\Rightarrow A\left(-1;0\right)\)
Đồ thị hàm số có 2 cực trị B, C nằm về 2 phía trục hoành khi và chỉ khi A nằm giữa B và C
\(\Rightarrow x_B< -1< x_C\) với \(x_B;x_C\) là nghiệm của pt \(f\left(x\right)=3x^2+6x+m=0\)
\(\Rightarrow3.f\left(-1\right)< 0\Leftrightarrow3\left(3-6+m\right)< 0\Rightarrow m< 3\)
Vậy với \(m< 3\) thì đồ thị hs có 2 cực trị nằm về 2 phía trục hoành
2/
\(y=x^3+3mx^2+m+1\Rightarrow y'=3x^2+6mx\)
Để hàm số có 2 cực trị \(\Rightarrow m\ne0\)
Chia đa thức \(y\) cho \(y'\) được phân dư \(-2m^2x+m+1\)
\(\Rightarrow\) phương trình đường thẳng \(d\) qua 2 cực trị có dạng:
\(y=-2m^2x+m+1\)
Để \(d\) song song đường thẳng \(y=-x+2017\)
\(\Rightarrow\left\{{}\begin{matrix}-2m^2=-1\\m+1\ne2017\end{matrix}\right.\) \(\Rightarrow m=\pm\dfrac{\sqrt{2}}{2}\)

Bài 1: Ta có
\(y'=0\Leftrightarrow x[2mx^2-(m+1)]=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ 2mx^2-(m+1)=0(1)\end{matrix}\right.\)
Một điểm nằm trên trục tọa độ thì tung độ hoặc hoành độ phải bằng $0$. Do đó yêu cầu đề bài được đáp ứng khi $y'=0$ có nghiệm $x=0$ hoặc nếu $x$ khác $0$ thì tung độ tương ứng phải bằng $0$
+) Nếu \(m=0\) : $(1)$ vô nghiệm . $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu $m=-1$ : $(1)$ có nghiệm $x=0$ (thỏa mãn)
+) Nếu $-1< m< 0$. Từ \((1)\Rightarrow x^2=\frac{m+1}{2m}< 0\) (vô lý) nên $(1)$ vô nghiệm. $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu \(m>0\) hoặc \(m< -1\)
$(1)$ có 2 nghiệm \(x=\pm \sqrt{\frac{m+1}{2m}}\neq 0\)
\(\Rightarrow y=m(\pm \sqrt{\frac{m+1}{2m}})^4-(m+1)(\pm \sqrt{\frac{m+1}{2m}})^2+(m+1)\)
\(=\frac{(m+1)^2}{4m}-\frac{(m+1)^2}{2m}+(m+1)\)
\(=(m+1)-\frac{(m+1)^2}{4m}=0\)
\(\Leftrightarrow \left[\begin{matrix} m=-1\\ m=\frac{1}{3}\end{matrix}\right.\) . Vì \(\Rightarrow m=\frac{1}{3}\)
Vậy \(-1\leq m\leq 1 \text{or m}=\frac{1}{3}\)
Bài 2:
Ta có: \(y'=4x^3+4mx=0\Leftrightarrow x(x^2+m)=0\)
Nếu $m\geq 0$. PT $y'=0$ có duy nhất nghiệm $x=0$. Ta chỉ thu được 1 điểm cực trị (loại)
Nếu $m<0$. Ngoài $x=0$ pt $y'=0$ còn có 2 nghiệm \(x=\pm \sqrt{-m}\neq 0\)
(thu được 3 cực trị)
Khi đó:
\(y=(\pm \sqrt{-m})^4+2m(\pm \sqrt{-m})^2+4=m^2-2m^2+4=4-m^2\)
Để điểm cực trị nằm trên trục tọa độ thì \(y=0\Leftrightarrow 4-m^2=0\Leftrightarrow m=-2\) (do $m< 0$)
Vậy \(m=-2\)

Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^

Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC

Đáp án B.
Phương trình hoành độ giao điểm của (C) và d : x − 2 x − 1 = − x + m
⇔ x ≠ 1 x − 2 = ( − x + m ) ( x − 1 ) ⇔ x ≠ 1 f ( x ) = x 2 − m x + m − 2 = 0 ( * )
Để (C) và d cắt nhau tại hai điểm phân biệt A, B khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x 1 , x 2 khác 1
⇔ f ( 1 ) = 1 2 − m + m − 2 ≠ 0 Δ = - m 2 − 4 ( m − 2 ) > 0 ⇔ − 1 ≠ 0 m 2 − 4 m + 8 m > 0 ⇔ m ∈ ℝ .
Mặt khác OAB là tam giác nên O ∈ d hay m ≠ 0 .
Gọi A ( x 1 ; − x 1 + m ) và B ( x 2 ; − x 2 + m ) . Suy ra O A = 2 x 1 2 − 2 m x 1 + m 2 O B = 2 x 2 2 − 2 m x 2 + m 2
Do x 1 , x 2 là hai nghiệm của phương trình (*) nên x 1 2 − m x 1 = 2 − m x 2 2 − m x 2 = 2 − m
Khi đó O A = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4 O B = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4
Từ giả thiết ta có :
2 m 2 − 2 m + 4 = 1 ⇔ m 2 − 2 m + 4 = 2 ⇔ m ( m − 2 ) = 0 ⇔ m = 0 m = 2
Đối chiếu với điều kiện ta được m=2 thỏa mãn.



Chọn A.
Xét PT hoành độ x 3 − 2 x 2 + 1 − m x + m = 0 (1)
Để C m cắt Ox tại 3 điểm có hoành độ là x 1 ; x 2 ; x 3 , tức PT (1) có 3 nghiệm phân biệt là x 1 ; x 2 ; x 3
Áp dụng vi –ét có : x 1 + x 2 + x 3 = − b a = − − 2 1 = 2 x 1 x 2 + x 2 x 3 + x 1 x 3 = c a = 1 − m 1 = 1 − m x 1 x 2 x 3 = − d a = − m 1 = − m
theo bài ta có
x 1 2 + x 2 2 + x 3 2 = 4 ⇔ x 1 + x 2 + x 3 2 − 2 x 1 x 2 + x 2 x 3 + x 1 x 3 = 4 ⇔ 2 2 − 2 1 − m = 4 ⇔ 4 − 2 + 2 m = 4 ⇔ 2 m = 2 ⇔ m = 1