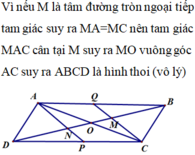
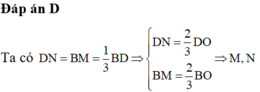Cho hình bình hành ABCD , trên đường chéo BD lấy 2 điểm M,N = MN = ND . a, cmr AMCN là hbh ; b, Gọi K là giao điểm của M & AB , H là gđ của AN & CD , O là trung điểm của MN , Cmr H,O,K thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Ta có D N = B M = 1 3 B D ⇒ D N = 2 3 D O B M = 2 3 B O ⇒ M , N lần lượt là trọng tâm tam giác ABC, ACD

Trả lời:
Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 1800 - AMD = 1800 - CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
a) => AMCN là hình bình hành
b)=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi
~Học tốt~
Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 180o - AMD = 180o- CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
=> AMCN là hình bình hành
=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi
Hok tốt !

Chọn D
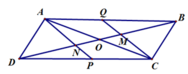
Vì nếu M là tâm đường tròn ngoại tiếp tam giác suy ra MA = MC nên tam giác MAC cân tại M suy ra MO vuông góc AC suy ra ABCD là hình thoi (vô lý)

ABCDMN
a) Vì tứ giác ABCD
=>AB//CD
=>^AMB=^CND (2 góc so le trong)
Xét t/gAMB và t/gCND ta có:
MB=DN (gt)
^AMB=^CND (cmt)
AB=CD ( hai cạnh đối của hbh = nhau)
b) quên vẽ điểm O vẽ hộ nhé
Vì AC cắt BD tại O
do đó: O là trung điểm của BD và AC
=>OA=OC (1)
=>OB=OD
Mà ta có: OD=OB (cmt)
mà DN=BM (gt)
do đó: ON=OM (2)
Từ (1) và (2) =>AMCN là hbh ( 2 đường chéo cắt nhau tại trung điểm)

Ta có \(2^2+4^2+6^2+...+20^2=2^2.\left(1^2+2^2+3^2+...+10^2\right)\)
Do đó S = 22M
=> M = 1540 . 22 = 1540 . 4 = 6160