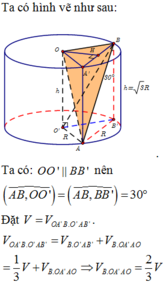
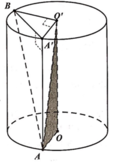
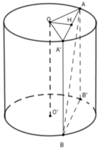
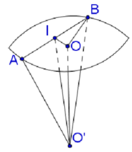
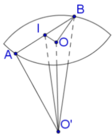
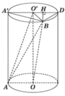
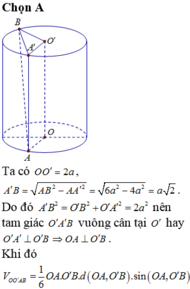
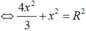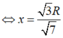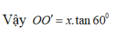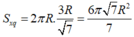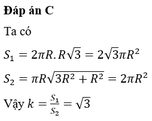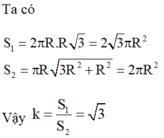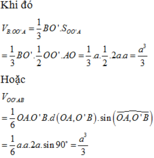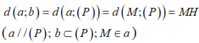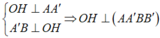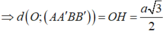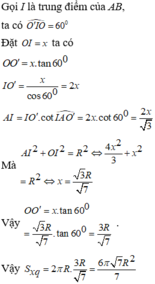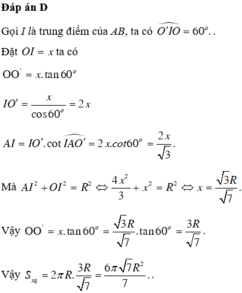Cho hình trụ có hai đáy là hai đường tròn (O;R) và (O';R), chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O' lấy điểm B. Thể tích của khối tứ diện OO'AB có giá trị lớn nhất bằng:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM
Cao Minh Tâm
17 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan

CM
28 tháng 12 2018
Đáp án D
Gọi I là trung điểm của AB, ta có ∠ O ' I O = 60 °
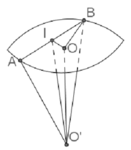
Đặt OI=x ta có:
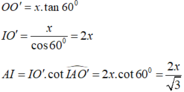
![]()