Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Gọi z = x + y i , x , y ∈ ℝ .
Ta có x 2 + y − 1 2 = 16, x = 0 ⇒ y = − 3 y = 5 .
Vậy có 2 số phức thỏa mãn đề bài
Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
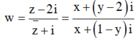
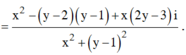
w là một số ảo
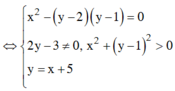
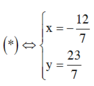
Vậy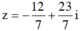 
Đặt z=x+yi ta có hệ đều kiện:
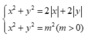
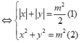
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
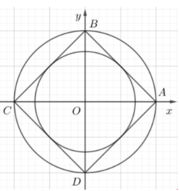
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông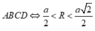 
Chọn đáp án D.
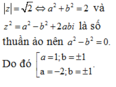
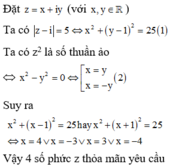
Đáp án A.