Tìm nguyên hàm của hàm số f ( x ) = 2 x + 1 .
A. ∫ f ( x ) d x = 1 2 2 x + 1 + C
B. ∫ f ( x ) d x = 2 3 2 x + 1 2 x + 1 + C
C. ∫ f ( x ) d x = - 1 3 2 x + 1 + C
D. ∫ f ( x ) d x = 1 3 2 x + 1 2 x + 1 + C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
3 tháng 3 2021
\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)
\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)
=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)
C=-1 ta được phương án A(ko tm câu hỏi)
C=0 ta được phương án B(ko tm câu hỏi)
C=2 ta được phương án C(ko tm câu hỏi)
=>chọn D
25 tháng 10 2021
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
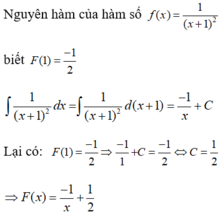
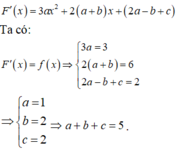
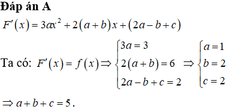
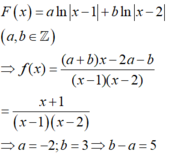
Chọn D
Đặt t = 2 x + 1 ⇒ d t = 1 2 x + 1 d x ⇒ d x = t d t
⇒ ∫ 2 x + 1 d x = ∫ t 2 d t = t 3 3 + C = 1 3 2 x + 1 2 x + 1 + C