Tìm giá trị cực đại y C Đ của hàm số y = x 3 − 3 x 2 + 3
A. y C Đ = 2
B. y C Đ = 0
C. y C Đ = 3
D. y C Đ = − 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.

\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Ta có tọa độ 3 cực trị: \(A\left(0;5\right)\) ; \(B\left(-1;4\right)\) ; \(C\left(1;4\right)\)
\(\overrightarrow{AB}=\left(-1;-1\right)\Rightarrow AB=\sqrt{2}\) ; \(\overrightarrow{AC}=\left(1;-1\right)\Rightarrow AC=\sqrt{2}\)
\(\overrightarrow{BC}=\left(2;0\right)\Rightarrow BC=2\)
Chu vi: \(AB+BC+AC=2+2\sqrt{2}\)

tưởng tượng đi hàm số đó có đạo hàm =0 lúc x= -2,-1,0
nghĩa là tìm x sao cho x^2-2X=-2,-1,0
=> giải 3 pt => có 3 nghiệm x => có 3 cực trị
ban co thể nói rỏ hơn được không để mình muốn vận dụng cho những bài biến tấu khác .. tks bạn nhiều

Đáp án: B.
Hàm số y = ( x + 1 ) 3 (5 - x) xác định trên R.
y' = - ( x + 1 ) 3 + 3 ( x + 1 ) 2 (5 - x) = 2 ( x + 1 ) 2 (7 - 2x)
y' = 0 ⇔ 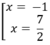
Bảng biến thiên
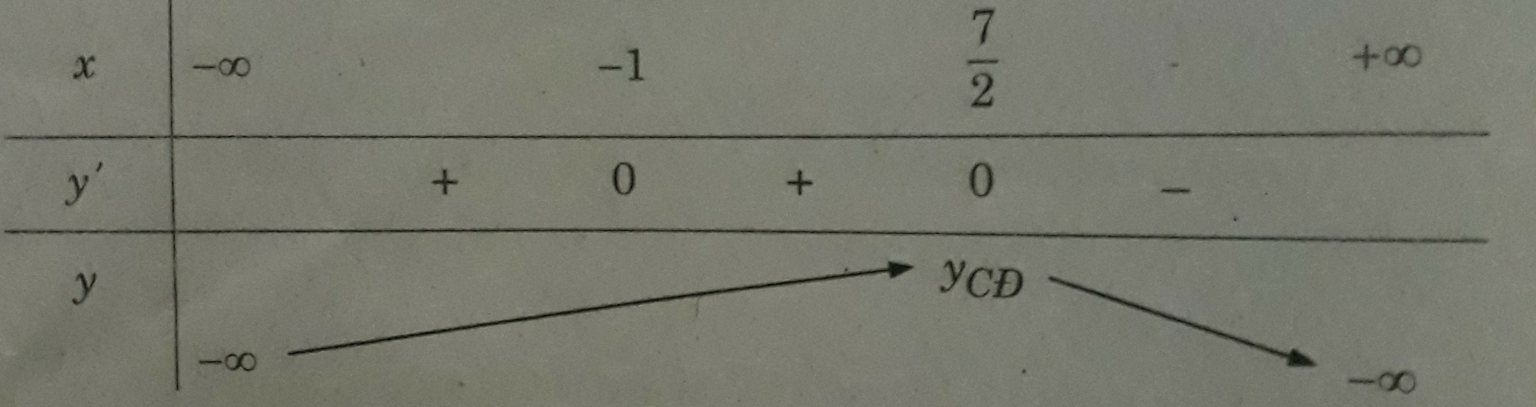
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị
Đáp án C
Ta có: y ' = 3 x 2 − 6 x ⇒ y ' = 0 ⇔ x = 0 x = 2
Mặt khác:
y ' ' = 6 x − 6 ⇒ y ' ' 0 = − 6 y ' ' 2 = 6 ⇒ y C Đ = y 0 = 3.