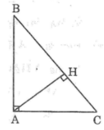
Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
Trực tâm của ΔABC là đỉnh A
Trực tâm của ΔAHB là đỉnh H
Trực tâm của ΔAHC là đỉnh H
3 tháng 3 2023
Xét ΔACB có
AK,BN là các đườg cao
AK cắt BN tại M
=>M là trực tâm
BB
19 tháng 10 2017
Đề bài có đủ điều kiện để tính. Sau khi xác định được tỷ lệ các cạnh tg ABC là a:b:c=5:4:3, đặt AB=3t, AC=4t; BC=5t (như bạn Hải đã chứng minh). Vì tam giác ABC vuông ta có AB^2=BH.BC ---> (3t)^2=BH.(5t) ---> BH=1,8.t
----> AH^2=AB^2-BH^2 =(3t)^2 -(1,8t)^2 = 9t^2 -3,24t^2 =5,76t^2 --> AH= 2,4t
Chu vi ABH=30 --> AB+BH+AH=30 --> 3t+1,8t+2,4t=30 --->7,2t=30 ---> t= 25/6
Chu vi ABC= 3t+4t+5t= 12t =12.(25/6) =50 cm
Chúc huyền luôn luôn học giỏi và sớm kiếm được nhiều k.
*Tam giác ABC có ∠(BAC) = 90o
Vì CA là đường cao xuất phát từ đỉnh C; BA là đường cao xuất phát từ đỉnh B
Và hai đường cao này cắt nhau tại A nên A là trực tâm của ΔABC.
*Tam giác AHB có ∠(AHB) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, BH là đường cao xuất phát từ đỉnh B và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHB.
*Tam giác AHC có ∠(AHC) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, CH là đường cao xuất phát từ đỉnh C và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHC.