Tìm số là ước chung lớn nhất của hai số và ().
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử 4 là ước chung của n+1 và 2n+5
Ta có n+1 \(⋮\)4 và 2n+5\(⋮\) 4
Suy ra (2n+5 )-(2n+2)\(⋮\)4,vô lí
Vậy số 4 không thể là ước chung của n+1 và 2n+5
Giả sử 4 là ước chung của \(n+1\) và \(2n+5\)
\(\Rightarrow\left\{{}\begin{matrix}n+1⋮4\\2n+5⋮4\end{matrix}\right.\)
\(\Rightarrow3⋮4\) \(\rightarrow\) vô lí
\(\Rightarrow4\) ko là ước chung của \(n+1\) và \(2n+5\)

Gọi d là ước chung của n+3 và 2n+5
Ta có n+3\(⋮\) d và 2n+5 \(⋮\)d
Suy ra (2n+6)-(2n+5)\(⋮\) d \(\Rightarrow\) 1\(⋮\)d
Vậy d=1
Gọi d là ước chung của n + 3 và 2n + 5.
Ta có n + 3 ⋮ d và 2n + 5 ⋮ d.
Suy ra (2n + 6) - (2n + 5) ⋮ d ⇒
1 ⋮ d.
Vậy d = 1.

b: Gọi d=UCLN(2n+1;3n+1)
\(\Leftrightarrow3\left(2n+1\right)-2\left(3n+1\right)⋮d\)
\(\Leftrightarrow1⋮d\)
=>d=1
=>UC(2n+1;3n+1)={1;-1}
c: Gọi d=UCLN(75n+6;8n+7)
\(\Leftrightarrow8\left(5n+6\right)-5\left(8n+7\right)⋮d\)
\(\Leftrightarrow d=13\)
=>UC(5n+6;8n+7)={1;-1;13;-13}

1. Gọi d là ước số chung của n+3 và 2n+5, d,n C N. Khi đó 2(n+3)-(2n+5) chia hết cho d hay 1 chia hết cho d, vậy d=1 hay 2 số n+3 và 2n+5 là 2 số nguyên tố cùng nhau
2. Nếu d là USC của n+1 và 2n+5 thì (2n+5)-2(n+1) chia hết cho d hay 3 chia hết cho d, vậy d=1 hoặc 3 do đó số 4 không thể là USC của 2 số n+1 và 2n+5

1. Gọi d là ước chung của n+3 và 2n+5
Ta có: n+3 \(⋮\)d , 2n+5\(⋮d\)
=> (2n+6)-(2n+5) chia hết cho d=> 1 chia hết cho d
Vậy ƯC của n+3 và 2n+5 là 1
2. giả sử 4 là ƯC của n+1 và 2n+5
Ta cs: n+1 \(⋮\)4 , 2n+5\(⋮\)4
=> (2n+5)-(2n+2) chia hết cho 4=> 3 chia hết cho 4(vô lý)
Vậy số 4 không thể là ƯC của n+1 và 2n+5.
Bạn ghét những đứa đặt tên dài, cậu có thể giải thích tại sao ở câu 1, n + 3=2n+6 được chứ, cả câu 2 n+1=2n+5 nữa. Cảm ơn!
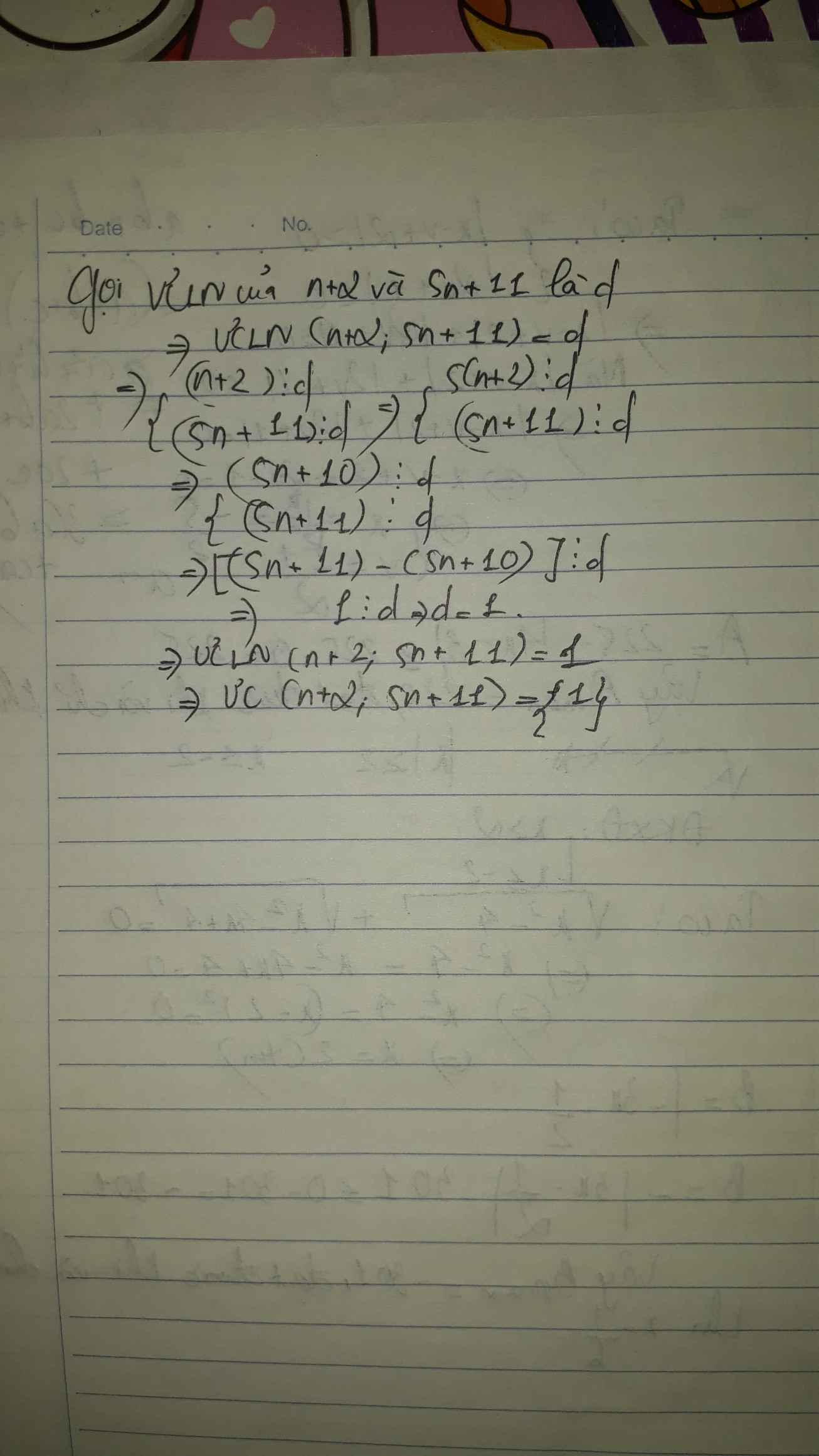
ƯCLN (n+2,5n+11)=d
=>d=ƯCLN (n+2,5(n+2)+1)=ƯCLN (n+2,1)=1
vậy d=1