Tìm x biết 1 , x 2 , 6 − x 2 lập thành cấp số nhân.
A. x = ± 1
B. x = ± 2
C. x = ± 2
D. x = ± 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2023
1: Để ba số này lập thành 1 cấp số nhân thì
\(\left[{}\begin{matrix}\left(x+4\right)^2=\left(4x+8\right)\left(x+2\right)\\\left(x+2\right)^2=\left(x+4\right)\left(4x+8\right)\\\left(4x+8\right)^2=\left(x+2\right)\left(x+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x+4\right)^2-\left(x+4\right)^2=0\\4x^2+8x+16x+32-x^2-4x-4=0\\16x^2+64x+64-x^2-6x-8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(2x+4-x-4\right)\left(2x+4+x+4\right)=0\\3x^2+20x+28=0\\15x^2+58x+56=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x\left(3x+8\right)=0\\x\in\left\{-2;-\dfrac{14}{3}\right\}\\x\in\left\{-\dfrac{28}{15};-2\right\}\end{matrix}\right.\)
=>\(x\in\left\{0;-\dfrac{8}{3};-\dfrac{14}{3};-\dfrac{28}{15}\right\}\)
2:
Để đây là 1 cấp số nhân thì
\(\left[{}\begin{matrix}1^2=5\left(2x+4\right)\\5^2=1\cdot\left(2x+4\right)\\\left(2x+4\right)^2=1\cdot5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}10x+20=1\\2x+4=25\\\left(2x+4\right)^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{19}{10}\\x=\dfrac{21}{2}\\2x+4=\pm\sqrt{5}\end{matrix}\right.\)
=>\(x\in\left\{-\dfrac{19}{10};\dfrac{21}{2};\dfrac{\sqrt{5}-4}{2};\dfrac{-\sqrt{5}-4}{2}\right\}\)
2 tháng 10 2023
1, Ta có \(\left(x+4\right)^2=\left(x+2\right)\left(4x+8\right)\Leftrightarrow x^2+8x+16=4x^2+12x+16\)
\(\Leftrightarrow3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
2, tương tự
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(2x - 1;x;2x + 1\) theo thứ tự lập thành cấp số nhân khi:
\({x^2} = \left( {2x - 1} \right)\left( {2x + 1} \right) \Leftrightarrow {x^2} = 4{{\rm{x}}^2} - 1 \Leftrightarrow 3{{\rm{x}}^2} - 1 = 0 \Leftrightarrow x = \pm \frac{{\sqrt 3 }}{3}\)
Vậy có 2 số thực \(x\) thoả mãn \(2x - 1;x;2x + 1\) theo thứ tự lập thành cấp số nhân.
Chọn B.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 9 2023
\(Bài.1:u_n=\dfrac{3}{2}.\left(\dfrac{1}{2}\right)^n=\dfrac{3}{512}\\ \Rightarrow\left(\dfrac{1}{2}\right)^n=\dfrac{3}{512}:\dfrac{3}{2}=\dfrac{1}{256}=\dfrac{1}{2^8}\\ Mà:\left(\dfrac{1}{2}\right)^n=\left(\dfrac{1}{2}\right)^8\\ Vậy:n=8\\ \Rightarrow Vậy:\dfrac{3}{512}.là.số.hạng.thứ.8\)
CM
30 tháng 6 2019
Chọn B.
+ Ta có các số 5x - y; 2x + 3y; x + 2y lập thành CSC nên suy ra
2( 2x + 3y) = 5x – y + x+ 2y hay 2x = 5y (1)
Các số (y + 1)2, xy + 1, (x – 1)2 lập thành CSN suy ra (xy + 1)2 = (y + 1)2(x – 1)2 ⇔ (4 + 2y – 2x)(4xy + 2x – 2y) = 0 (2)
Thay (1) vào (2) ta được: (4 + 2y – 5y)(10y2 + 5y – 2y) = 0
⇔ y(4 – 3y)(10y + 3) = 0 ⇔ y = 0, y = 4/3, y = -3/10.
Vậy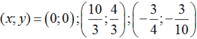 
XC
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Để 3 số 3, x + 2, 12 lập thành 1 dãy cấp số nhân thì:
\(\left(x+2\right)^2=3\cdot12\\ \Rightarrow\left(x+2\right)^2=36\\ \Leftrightarrow\left[{}\begin{matrix}x+2=6\\x+2=-6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)
Vậy \(x\in\left\{-8;4\right\}\)
12 tháng 9 2023
1: Để đây là cấp số cộng thì
\(\left\{{}\begin{matrix}x=\dfrac{2+8}{2}=\dfrac{10}{2}=5\\8=\dfrac{y+x}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y+5=16\end{matrix}\right.\)
=>x=5 và y=11
2: Để bốn số này là cấp số cộng thì
\(\left\{{}\begin{matrix}a+b+1=2\cdot5=10\\b+1=\dfrac{5+13}{2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\a=1\end{matrix}\right.\)
21 tháng 4 2016
Theo giả thiết ta có : \(\begin{cases}\left(5x-y\right)+\left(x+2y\right)=2\left(2x+3y\right)\\\left(y+1\right)^2\left(x-1\right)^2=\left(xy+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\xy+x+y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\y\left(5y\right)+5y+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{10}{3}\\y=\frac{4}{3}\end{cases}\) hoặc \(\begin{cases}x=0,y=0\\x=-\frac{3}{4},y=-\frac{3}{10}\end{cases}\)
Ta có: 1 , x 2 , 6 − x 2 lập thành cấp số nhân khi và chỉ khi:
x 2 2 = 1. ( 6 − x 2 ) ⇔ x 4 = 6 − x 2 ⇔ x 4 + x − 2 6 = 0 ⇔ x 2 = 2 ⇔ x = ± 2
Chọn đáp án B.