16x2 - y2; 6x2 - 11x + 3. Phân tích đa thức thành nhân tử
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2021
câu 1 B
câu 2 D
câu 3 ko bt
câu 4 x=-1/2; x = -(căn bậc hai(3)*i-1)/4;x = (căn bậc hai(3)*i+1)/4;
câu 5 x=-5/3, x=0, x=1
23 tháng 11 2021
Câu 1: x2 + 2 xy + y2 bằng:
A. x2 + y2 B.(x + y)2 C. y2 – x2 D. x2 – y2
Câu 2: (4x + 2)(4x – 2) bằng:
A. 4x2 + 4 B. 4x2 – 4 C. 16x2 + 4 D. 16x2 – 4
Câu 3: 25a2 + 9b2 - 30ab bằng:
A.(5a-9b)2 B.(5a – 3b)2 C.(5a+3b)2 D.(5a)2 – (3b)2
Câu 4: 8x3 +1 bằng
A.(2x+1).(4x2-2x+1) B. (2x-1).(4x2+2x+1) C.(2x+1)3 D.(2x)3-13
Câu 5:Thực hiện phép nhân x(3x2 + 2x - 5) ta được:
A.3x3 - 2x2 – 5x B. 3x3 + 2x2 – 5x C. 3x3 - 2x2 +5x D. 3x3 + 2x2 + 5x
4 tháng 10 2021
\(16x^2-8xy+y^2+1=\left(4x-y\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow4x=y\)
\(-4x^2+2x-1=-\left(4x^2-2\cdot2\cdot\dfrac{1}{2}x+\dfrac{1}{16}\right)-\dfrac{15}{16}=-\left(2x-\dfrac{1}{4}\right)^2-\dfrac{15}{16}\le-\dfrac{15}{16}\)
Dấu \("="\Leftrightarrow2x=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{8}\)
48
1
10 tháng 10 2021
\(6x^3-9x^2=3x^2\left(2x-3\right)\\ 25x^2-0,09=\left(5x-0,3\right)\left(5x+0,3\right)\\ x^2-x-y^2-y=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\\ \left(x^2+4\right)^2-16x^2=\left(x^2-4x+4\right)\left(x^2+4x+4\right)=\left(x-2\right)^2\left(x+2\right)^2\)
VD
2
12 tháng 9 2021
\(a,=5\left(x^3+8y\right)\\ b,=\left(4x+y\right)^2-16=\left(4x+y-4\right)\left(4x+y+4\right)\\ c,=3\left(x^2+2\cdot\dfrac{7}{3}x-5\right)\\ =3\left(x^2+2\cdot\dfrac{7}{3}x+\dfrac{49}{9}-\dfrac{94}{9}\right)\\ =3\left(x+\dfrac{7}{3}-\dfrac{\sqrt{94}}{3}\right)\left(x+\dfrac{7}{3}+\dfrac{\sqrt{94}}{3}\right)\)
12 tháng 9 2021
a: \(5x^3+40y=5\left(x^3+8y\right)\)
b: \(16x^2+8xy+y^2-16\)
\(=\left(4x+y\right)^2-16\)
\(=\left(4x+y-4\right)\left(4x+y+4\right)\)
CM
23 tháng 11 2019
Ta có: x y − 3 x − 2 y = 16 x 2 + y 2 − 2 x − 4 y = 33 1
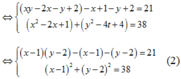
Đặt u = x − 1 , v = y − 2 ta được h
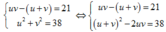
Đặt S = u + v, P = uv ta được hệ P − S = 21 S 2 − 2 P = 38 ⇔ P = S + 21 S 2 − 2 S − 80 = 0
⇔ S = − 8 P = 13 hoặc S = 10 P = 31
+ Khi ⇔ S = − 8 P = 13 thì u, v là nghiệm của phương trình X 2 + 8 X + 13 = 0
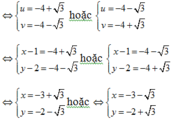
+ Khi S = 10 P = 31 thì u, v là nghiệm của phương trình X 2 - 10 X + 31 = 0 (vô nghiệm)
Vậy hệ có nghiệm x ; y = − 3 − 3 ; − 2 + 3 x ; y = − 3 + 3 ; − 2 − 3
Đáp án cần chọn là: A
CM
4 tháng 6 2019
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính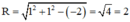 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
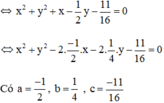
⇒ Đường tròn có tâm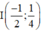 
, bán kính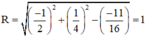 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính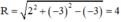 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
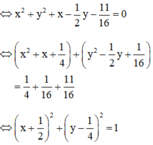
Vậy đường tròn có tâm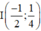 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{49}{16}\)
\(M_{min}=\dfrac{49}{16}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{\sqrt{7}};\dfrac{2}{\sqrt{14}};\dfrac{2}{\sqrt{7}}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{7}{4}\)
\(M_{min}=\dfrac{7}{4}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{\sqrt{2}};1\right)\)
5 tháng 10 2021
Bài 1:
a: \(11x^2-6xy-5y^2\)
\(=11x^2-11xy+5xy-5y^2\)
\(=11x\left(x-y\right)+5y\left(x-y\right)\)
\(=\left(x-y\right)\left(11x+5y\right)\)
b: \(4x^3-16x^2+19x-6\)
\(=4x^3-8x^2-8x^2+16x+3x-6\)
\(=\left(x-2\right)\left(4x^2-8x+3\right)\)
\(=\left(x-2\right)\left(2x-1\right)\left(2x-3\right)\)
Bài làm :
Ta có :
6x3 - 11x2 - x - 2
= 6x3 - 12x2 + x2 - 2x + x - 2
= ( 6x3 - 12x2 ) + ( x2 - 2x ) + ( x - 2 )
= 6x2( x - 2 ) + x( x - 2 ) + 1( x - 2 )
= ( x - 2 )( 6x2 + x + 1 ) nhớ tích