Cho hàm số y = f(x) xác định trên D . Với , ∈ D; < khẳng định nào sau đây là đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


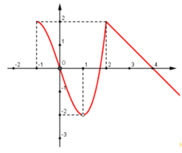
Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 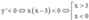 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞

Cho hàm số y = f ( x ) xác định trên tập D. Khi đó:
- Hàm số đồng biến trên D x 1 ; x 2 D ; x 1 > x 2 f ( x 1 ) > f ( x 2 ) .
- Hàm số nghịch biến trên D x 1 ; x 2 D ; x 1 > x 2 f ( x 1 ) < f ( x 2 ) .
Đáp án cần chọn là: C

Đáp án A
Cho hàm số y = f(x) xác định trên tập D. Khi đó:
• Hàm số đồng biến trên D ⇔ ∀ x 1 , x 2 ∈ D : x 1 < x 2 ⇒ f( x 1 ) < f( x 2 )
• Hàm số nghịch biến trên D ⇔ ∀ x 1 , x 2 ∈ D : x 1 < x 2 ⇒ f( x 1 ) > f( x 2 )

Cho hàm số xác định trên tập D. Khi đó:
- Hàm số đồng biến trên D x 1 ; x 2 D ; x 1 < x 2 f ( x 1 ) < f ( x 2 ) .
- Hàm số nghịch biến trên D x 1 ; x 2 D ; x 1 < x 2 f ( x 1 ) > f ( x 2 ) .
Đáp án cần chọn là: A

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 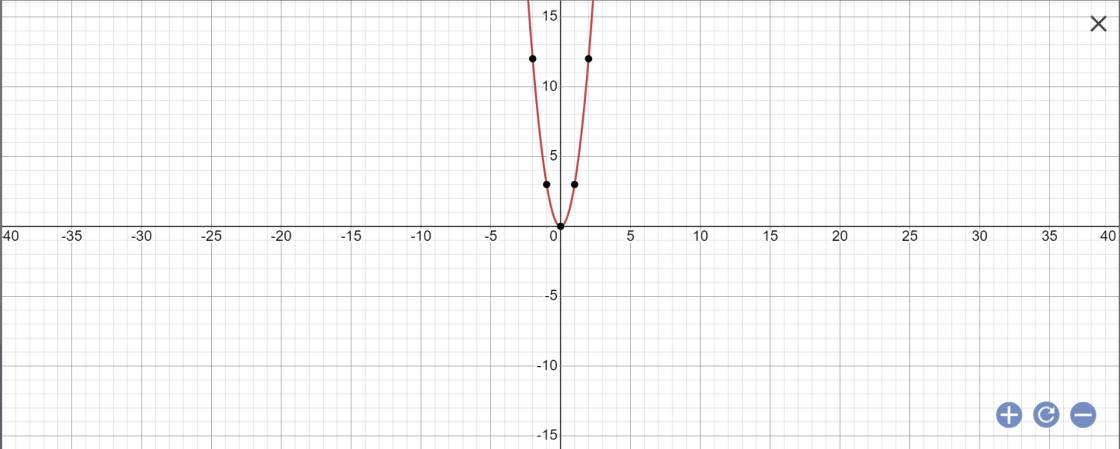

Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )
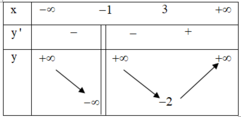


Đáp án A
Cho hàm số y = f(x) xác định trên tập D. Khi đó:
• Hàm số đồng biến trên D ⇔ ∀ x 1 , x 2 ∈ D : x 1 < x 2 ⇒ f( x 1 ) < f( x 2 )
• Hàm số nghịch biến trên D ⇔ ∀ x 1 , x 2 ∈ D : x 1 < x 2 ⇒ f( x 1 ) > f( x 2 )