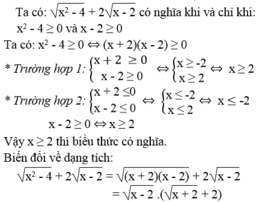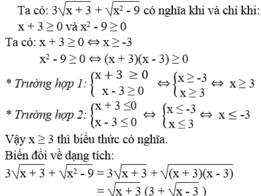Tìm điều kiện của các biến để các phân thức sau có nghĩa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 5 2018
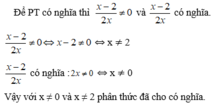
Để phân thức có nghĩa:
x 2 + 5 x + 4 ≠ 0
⇔ (x + 4)(x + 1) ≠ 0
⇔ x ≠ -4, x ≠ -1
Vậy điều kiện để phân thức xác định là x ≠ -4 và x ≠ -1
CM
6 tháng 12 2017
Để phân thức xác định ta có: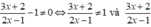 
có nghĩa:
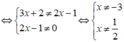
Vậy với x ≠ -3 và x ≠ ½ thì phân thức đã cho được xác định
11 tháng 11 2021
\(\dfrac{x}{4+2a}\) có nghĩa khi \(a\ne-2\)
\(\dfrac{y}{4-2a}\)có nghĩa khi \(a\ne2\)
\(\dfrac{z}{4-a^2}\)có nghĩa khi \(a\ne\pm2\)
MTC: \(2\left(2+a\right)\left(2-a\right)\)
C
26 tháng 10 2023
`sqrt(x-5)` có nghĩa khi:
`x-5 ≥0`
`=> x ≥5`
Vậy `x≥5` thì `sqrt(x-5` có nghĩa
____________
`1/(sqrt(3x-2))` có nghĩa khi
`1/(sqrt(3x-2)) ≥0`
`⇒ 3x-2≥0`
` ⇒3x≥2`
` ⇒x≥2/3`
Vậy `x ≥2/3` thì `1/(sqrt(3x-2))` có nghĩa
27 tháng 10 2023
Nếu x = 2/3 thì mẫu bằng 0 vậy biểu thức vẫn không có nghĩa thế bài làm vậy là đúng à
PT
1
CM
19 tháng 5 2017
Điều kiện để phân thức xác định là:
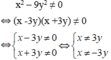
Vậy với x ≠ 3y và x ≠ -3y thì phân thức đã cho có nghĩa
AT
14 tháng 7 2021
Để \(\sqrt{x^2+3}\) có nghĩa thì \(x^2+3\ge0\) (luôn đúng)
Để \(\sqrt{\left(x-1\right)\left(x+2\right)}\) có nghĩa thì \(\left(x-1\right)\left(x+2\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-2\end{matrix}\right.\)
14 tháng 7 2021
a) ĐKXĐ: \(x\in R\)
b) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\)