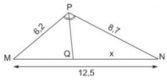
Tính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vì AD là phân giác của góc BAC
=>\(\dfrac{DC}{BD}=\dfrac{AC}{AB}\) <=>\(\dfrac{x}{3.5}=\dfrac{7.2}{4.5}\) <=>x=\(\dfrac{7.2X3.5}{4.5}\) <=>x=5.6
b)vì PQ là phân giác của góc MPN
=>\(\dfrac{QN}{MQ}=\dfrac{PN}{PM}\) <=>
a) AD là tia phân giác của ∆ABC nên
BDABBDAB = DCACDCAC => DC = BD.ACABBD.ACAB = 3,5.7,24,53,5.7,24,5
=> x = 5,6
b) PQ là đường phân giác của ∆PMN nên MQMPMQMP = NQNPNQNP
Hay MP6,2MP6,2 = x8,7x8,7
Áp dụng tính chất của tỉ lệ thức:
=> x8,7x8,7 = MP6,2

Bài 1:
\(S_{hcn}=94,54\cdot21,02\approx1987,2\left(m^2\right)\)

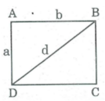
Giả sử hình chữ nhật ABCD có AB = b = 5cm; AD= a = 3cm; BD = d.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
d 2 = a 2 + b 2
⇒ d 2 = 3 2 + 5 2 = 9 + 25 = 34
Vậy 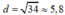 (cm).
(cm).

Theo định lý Py-ta-go :
\(d^2=a^2+b^2=3^2+5^2=34\)
hay \(d=\sqrt{34}\approx5,8\left(cm\right)\)
Giả sử hình chữ nhật ABCD có AB = a = 3cm; BC = b = 5cm; BD = d
Trong tam giác vuông ABC theo định lý Py-ta-go ta có:
d2=a2+b2⇒d2=32+52=9+25=34d=√34≈5,8(cm)
Ta có: MQ + QN = MN nên MQ = MN - QN = 12,5 - x
ΔPMN có PQ là phân giác
⇔ 8,7.(12,5 – x) = x.6,2
⇔ 108,75 – 8,7.x = 6,2.x
⇔ 108,75 = 14,9x hay 14,9.x = 108,75
⇔ x ≈ 7,3.