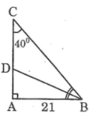
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()



Xét ΔABC vuông tại A có
tan C=AB/AC
=>21/AC=tan 40
=>\(AC\simeq25,03\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}\simeq32,67\left(cm\right)\)

a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)

a) Ta có:
\(sin40=\dfrac{AB}{BC}=\dfrac{21}{BC}\)\(\Rightarrow BC=\dfrac{21}{sin40}\simeq33cm\)
\(cos40=\dfrac{AC}{BC}\Rightarrow AC=cos40.33\simeq25cm\)
b) \(sinB=\dfrac{AC}{BC}=\dfrac{25}{33}\Rightarrow\widehat{B}\simeq49^o\)
\(BD=\dfrac{2.BC.AB.cos24,5}{BC+AB}\simeq12cm\)
\(Taco.\dfrac{BC}{sinA}=\dfrac{AB}{SinC}\Rightarrow BC=32,67cm=>AC=\sqrt{32,67^2-21^2}=25cm\)
Taco ^B=90-40=30 do
\(BD=\dfrac{2.21.32,67}{21+32,67}.CosB:2=24,69cm\)

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{10\sqrt{3}}{3}\right)^2=\dfrac{400}{3}\)
hay \(BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)