Rút gọn các phân thức: x 2 + 5 x + 6 x 2 + 4 x + 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
22 tháng 7 2023
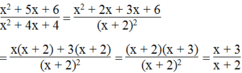
a) \(\dfrac{3x^2+6xy}{6x^2}=\dfrac{3x\left(x+2y\right)}{6x^2}=\dfrac{x+2y}{2x}\)
b) \(\dfrac{2x^2-x^3}{x^2-4}=\dfrac{x^2\left(2-x\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{-x^2}{x+2}\)
c) \(=\dfrac{x+1}{x^3+1}=\dfrac{x+1}{\left(x+1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
22 tháng 7 2023
`a, (3x^2+6xy)/(6x^2) = (x+2y)/(3x)`
`b, (2x^2-x^3)/(x^2-4) = (x^2(2-x))/((x-2)(x+2))`
`= -x^2/(x+2)`
`c, (x+1)/(x^3+1) = 1/(x^2-x+1)`
B
0
TK
1
18 tháng 12 2021
\(a,=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}=\dfrac{x+1}{x}\\ b,=\dfrac{-\left(x^2-5x-6\right)}{\left(x+2\right)^2}=\dfrac{-\left(x+1\right)\left(x-6\right)}{\left(x+2\right)^2}\)
BT
2
15 tháng 3 2020
a kham khảo nha , e nhờ a e lm chứ ko phải e lm nha !
\(\left(x-2\right)\left(\frac{3}{x}+2-\frac{5}{2x}-4+\frac{8}{x^2}-4\right)\)
\(\left(x-2\right)\left[\left(\frac{3}{x}-\frac{5}{2x}\right)-6+\frac{8}{x^2}\right]\)
\(\left(x-2\right)\left(\frac{1}{2x}-6+\frac{8}{x^2}\right)\)
15 tháng 3 2020
\(\left(x-2\right)\left(\frac{3}{x+2}-\frac{5}{2x-4}+\frac{8}{x^2-4}\right)\)
\(=\left(x-2\right)\left[\frac{3}{x+2}-\frac{5}{2\left(x-2\right)}+\frac{8}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{3.2\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{8.2}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)-5\left(x+2\right)+16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\frac{\left(x-2\right)\left(x-6\right)}{2\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x-6}{2\left(x+2\right)}\)
AD
23 tháng 7 2023
\(a,=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.\sqrt{2}+\left(\sqrt{2}\right)^2}\\ =\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{3}-\sqrt{2}\right|\\ =\sqrt{3}+\sqrt{2}-\left(\sqrt{3}-\sqrt{2}\right)\\ =\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\\=2\sqrt{2} \)
\(b,=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1}+\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1}\\ =\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =\left|\sqrt{3}+1\right|+\left|\sqrt{3}-1\right|\\ =\sqrt{3}+1+\sqrt{3}-1\\ =2\sqrt{3}\)
\(c,=x-4+\sqrt{\left(4^2-2.4.x+x^2\right)}\\ =x-4+\sqrt{\left(4-x\right)^2}\\ =x-4+\left|4-x\right|\\ =x-4+x-4=2x-8\) (vì \(x>4\) )
@seven
VI
2
13 tháng 6 2016
\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\left(DK:x\ne-1;x\ne1\right)\)
\(=\frac{x^4\left(x^3+x^2+x+1\right)+\left(x^3+x^2+x+1\right)}{x^2-1}\)
\(=\frac{x^4\left[x\left(x^2+1\right)+x^2+1\right]+\left[x\left(x^2+1\right)+x^2+1\right]}{x^2-1}\)
\(=\frac{\left(x^4+1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{\left(x^2+1\right)\left(x^4+1\right)}{x-1}\)
13 tháng 6 2016
\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\)
\(=\frac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{\left(x+1\right)\left(x^6+x^4+x^2\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^6+x^4+x^2}{x+1}\)
\(=\frac{x^2\left(x^3+x^2+1\right)}{x+1}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
1.
\(A=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+4\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9-\left(x^2-9\right)+\left(2x^2-8\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+2x-8}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-2\right)\left(x+4\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x+4}{x-3}\)
b.
\(A=2\Rightarrow\dfrac{x+4}{x-3}=2\Rightarrow x+4=2\left(x-3\right)\)
\(\Rightarrow x=10\) (thỏa mãn)
2.
\(x^4+2x^2y+y^2-9=\left(x^2+y\right)^2-3^2=\left(x^2+y-3\right)\left(x^2+y+3\right)\)
20 tháng 12 2022
Câu 4: Không có nghĩa khi x-3=0
=>x=3
Câu 5:
\(A=\dfrac{x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)
NA
0