Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD

Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.


Lời giải:
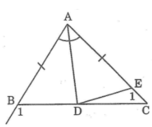
Trên cạnh AC lấy điểm E sao cho AE = AB.
Ta có: AB < AC nên AE < AC
Suy ra E nằm giữa A và C.
Xét ΔABD và ΔAED, ta có:
AB = AE (theo cách vẽ)
∠(BAD) = ∠(EAD) (gt)
AD cạnh chung
Suy ra: ΔABD = ΔAED (c.g.c)
Suy ra: BD = DE (2 cạnh tương ứng)
và ∠(ABD) = ∠(AED) (2 góc tương ứng)
Mà: ∠(ABD) + ∠B1= 180o (2 góc kề bù)
∠(AED) + ∠E1= 180o (2 góc kề bù)
Suy ra: ∠B1= ∠E1
Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B
Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)
Suy ra: ∠E1> ∠C
Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Vậy BD < DC.
Trên cạnh AC lấy điểm E sao cho AE = AB
AB < AC nên AE < AC => E nằm giữa A và C
Xét ∆ABD và ∆AED:
AB = AE (theo cách vẽ)
\(\widehat{BAD}=\widehat{EAD}\left(gt\right)\)
AD cạnh chung
Do đó: ∆ABD = ∆AED (c.g.c)
=> BD = DE (2 cạnh tương ứng)
\(\Rightarrow\widehat{ABD}=\widehat{AED}\)(2 góc tương ứng)
\(\widehat{ABD}+\widehat{B_1}=180^0\)(2 góc kề bù)
\(\widehat{AED}+\widehat{E1}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{B_1}=\widehat{E_1}\)
Trong ∆ABC ta có\(\widehat{B_1}\)là góc ngoài tại đỉnh B.
\(\Rightarrow\widehat{B_1}>\widehat{C}\)(tính chất góc ngoài tam giác)
\(\Rightarrow\widehat{E_1}>\widehat{C}\)
Trong ∆DEC ta có:\(\widehat{E_1}>\widehat{C}\)
=>DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Suy ra: BD < DC

A B C E D 2 1 1 2 1 2
Lấy điểm E trên AC sao cho AE = AB.
Xét hai tam giác \(\Delta ABD\)và \(\Delta AED\),ta có :
AB = AE (gt)
\(\widehat{A_2}=\widehat{A_1}\)(vì AD là tia phân giác)
AD chung
Do đó : \(\Delta ABD=\Delta AED\left(c.g.c\right)\Rightarrow BD=DE\)
\(\widehat{B_1}=\widehat{E_1}\Leftrightarrow\widehat{B_2}=\widehat{E_2}\) (1)
Mặt khác,ta lại có : \(\widehat{B_2}>\widehat{C}\)(vì góc B2 là góc ngoài của tam giác ABC) (2)
Từ (1) và (2) suy ra : \(\widehat{E_2}>\widehat{C}\)
Khi đó trong \(\Delta CDE\)vì : \(\widehat{E_2}>\widehat{C}\Leftrightarrow CD>DE\Leftrightarrow CD>BD\)

b: Xét ΔBDE và ΔBCE có
BD=BC
\(\widehat{DBE}=\widehat{CBE}\)
BE chung
Do đó: ΔBDE=ΔBCE
c: Ta có: ΔBDC cân tại B
mà BF là đường phân giác
nên F là trung điểm của CD và BF\(\perp\)CD
Trên cạnh AC lấy điểm E sao cho AE = AB.
Ta có: AB < AC nên AE < AC
Suy ra E nằm giữa A và C.
Xét ΔABD và ΔAED, ta có:
AB = AE (theo cách vẽ)
∠(BAD) = ∠(EAD) (gt)
AD cạnh chung
Suy ra: ΔABD = ΔAED (c.g.c)
Suy ra: BD = DE (2 cạnh tương ứng)
và ∠(ABD) = ∠(AED) (2 góc tương ứng)
Mà: ∠(ABD) + ∠B1= 180o (2 góc kề bù)
∠(AED) + ∠E1= 180o (2 góc kề bù)
Suy ra: ∠B1= ∠E1
Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B
Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)
Suy ra: ∠E1> ∠C
Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Vậy BD < DC.