BD là đường phân giác của tam giác ABC. Chứng minh rằng B D 2 = AB.BC - AD.DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 12 2019
A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\) . Tia Cx cắt BD tại E
+ \(\Delta ABD~\Delta ECD\left(g.g\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{cases}}\)
\(\Rightarrow AD.CD=BD.ED\left(1\right)\)
+ \(\Delta ABD~\Delta EBC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB.BC=EB.BD\left(2\right)\)
Từ (1) và (2) suy ra
\(AB.BC-AD.DC=BD.EB-BD.ED=BD^2\)
20 tháng 5 2017
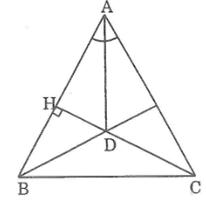
A B C H D b a
Vì câu a dễ nên mik chỉ làm câu b thôi nhé --hơi dài đấy , cần kiên nhẫn đọc--hoặc tham khảo cách nào ngắn gọn hơn cũng được , hình chỉ minh họa , độ chính xác ko cao
====================
Kẻ BH là đường cao của tam giác ABC
\(\Delta BAD\) cân tại B ( BA=BD) có BH là đường cao nên cũng là đường trung tuyến
=> AH = \(\frac{AD}{2}\)
\(\Delta ABC\) có BD là đường phân giác trong nên : \(\frac{DA}{DC}=\frac{AB}{BC}=\frac{b}{a}\)
=>\(\frac{DA}{b}=\frac{DC}{a}=\frac{DA+DC}{a+b}=\frac{AC}{a+b}=\frac{b}{a+b}\)=> \(DA=\frac{b^2}{a+b}\)
\(\Delta HAB\) vuông tại H , theo định lí Pi - ta - go ta có :
AB2 = BH2 + AH2 => BH2 = AB2 -AH2 = \(b^2-\frac{AD^2}{4}\) (1)
\(\Delta HBC\) vuông tại H , theo định lí Pi-ta-go , ta suy ra :
BH2 = BC2 - HC2 = BC2 - (AC - AH)2 = \(a^2-\left(b-\frac{AD}{2}\right)^2\)= \(a^2-b^2+b.AD-\frac{AD^2}{4}\left(2\right)\)
Từ (1) và (2) ta suy ra :
\(b^2-\frac{AD^2}{4}\) = \(a^2-b^2+b.AD-\frac{AD^2}{4}\left(2\right)\)
<=> \(b^2-a^2=b.AD-b^2\)
<=>\(\left(b-a\right)\left(b+a\right)=b.\frac{b^2}{a+b}-b^2\)
<=>\(\left(b-a\right)\left(b+a\right)=\frac{-ab^2}{a+b}\)
<=>\(\frac{a-b}{ab}=\frac{b}{\left(a+b\right)^2}\)
<=>\(\frac{1}{a}-\frac{1}{b}=\frac{b}{\left(a+b\right)^2}\) (đpcm)
HP
21 tháng 5 2017
Sao cách của bn giống hệt sách kẻ thêm hình phụ của nguyễn đức tấn nhỉ :)))
Y
14 tháng 5 2019
A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\). Tia Cx cắt BD tại E
+ ΔABD ∼ ΔECD ( g.g )
\(\Rightarrow\left\{{}\begin{matrix}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{matrix}\right.\)
=> \(AD\cdot CD=BD\cdot ED\) (1)
+ ΔABD ∼ ΔEBC ( g.g )
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB\cdot BC=BD\cdot EB\) (2)
+ Từ (1) và (2) suy ra : \(AB\cdot BC-AD\cdot CD=BD\cdot EB-BD\cdot ED=BD^2\)
PT
Cho tam giác ABC vuông tại A. Gọi BD là đường phân giác của góc B (D ∈ AC). Chứng minh rằng BD < BC.
1
CM
27 tháng 7 2019
Do BD là tia phân giác của góc ABC nên tia BD ở giữa hai tia BA và BC, suy ra D ở giữa A và C, hay AD < AC.
Hai đường xiên BC, BD lần lượt có hình chiếu trên AC là AC và AD.
Mà AD < AC, suy ra BD < BC.
25 tháng 12 2016
Mình vẽ nhầm hình nha, để mình vẽ lại ở dưới cái nào để chữ vẽ lại thì bạn vẽ cái đó
Đây là bài làm
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đói đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
30 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
BD=CE
góc ABD=góc ACE
=>ΔADB=ΔAEC
=>AB=AC
=>ΔABC cân tại A
b: ΔABC cân tại A
mà AD là đường phân giác
nên AD vuông góc BC
Xét ΔABC có
AD,CH là đường cao
AD cắt CH tại D
=>D là trực tâm
=>BD vuông góc AC
Gọi E là giao điểm của tia BD với đường tròn ngoại tiếp tam giác ABC.