Cho hình vẽ:
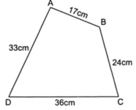
Chu vi của hình tứ giác ABCD là:
A. 110cm
B. 100dm
C. 110dm
D. 100cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:
AB2=OA2+OB2
AB2=42+32 = 16 + 9 = 25
AB = √25
Vậy chu vi của hình thoi bằng 4√25

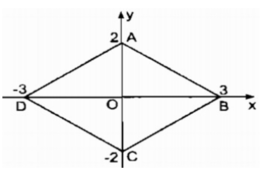
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13

a)nửa chu vi HCN ABCD là : 100 : 2 = 50 ( cm )
nửa chu vi HCN BMNC là : 60 : 2 = 30 ( cm )
cạnh hình vuông ANND là : 50 - 30 = 20 ( cm ) _vẽ hình rồi hiểu
chiều dài HCN ABCD là : 50 - 20 = 30 ( cm )
b) diện tích DMC là :
30 x 20 : 2 = 300 ( cm2 )
ĐS:...
_HT_
#ThaoNguyen#

Vì AMND là hình vuông có cạnh bằng chiều rộng hình chữ nhật ABCD nên chu vi hình chữ nhật BMNC chính bằng 2 lần chiều dài hình chữ nhật ABCD
Chiều dài hình chữ Nhật ABCD là
60:2=30(cm)
Chiều rộng hình chữ Nhật ABCD là
100:2-30=20(cm)
Diện tích Tam giác DMC là
20x30:2=300(cm2)
Chiều dài MB là
30-20=10(cm)
Diện tích Tam giác DMB là
20x10:2=100(cm2)
( đường cao DA=20cm, đáy MB=10cm)

Vì AMND là hình vuông có cạnh bằng chiều rộng hình chữ nhật ABCD nên chu vi hình chữ nhật BMNC chính bằng 2 lần chiều dài hình chữ nhật ABCD Chiều dài hình chữ Nhật ABCD là 60:2=30(cm) Chiều rộng hình chữ Nhật ABCD là 100:2-30=20(cm) Diện tích Tam giác DMC là 20x30:2=300(cm2) Chiều dài MB là 30-20=10(cm) Diện tích Tam giác DMB là 20x10:2=100(cm2) ( đường cao DA=20cm, đáy MB=10cm)

Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên
Đáp án A