Tìm giá trị lớn nhất của hàm số trên đoạn [0; 2]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C.
• Ta có: y , = 1 2 x + 1 - 1 2 3 - x , cho y , = 0 ⇔ x = 1 ∈ - 1 ; 3
• Tính được: y ( - 1 ) = 2 ; y ( 3 ) = 2 ; y ( 1 ) = 2 2
Vậy m a x y [ - 1 ; 3 ] = 2 2

Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
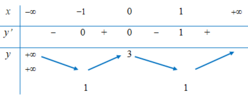
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

Chọn đáp án A
Từ giả thiết
![]()
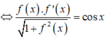

![]()
![]()
Suy ra
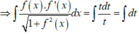
![]()
Từ (1) và (2) suy ra 1 + f 2 x = sin x + C
Thay x = 0 vào ta được:
![]()
do f 0 = 3
Suy ra
![]()
![]()
![]()
do hàm số f x liên tục, không âm trên 0 ; π 2
Đặt t = sin x
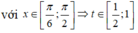
Xét hàm số g t = t 2 + 4 t + 3 trên 1 2 ; 1
Ta có

⇒ Hàm số g t đồng biến trên 1 2 ; 1
Khi đó
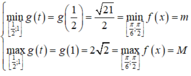

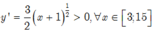
=> Hàm số đã cho đồng biến trên đoạn [ 3; 15].
Hàm số đạt giá trị lớn nhất tại x= 15 và M= y (15) = 64
Chọn A.

Chọn A
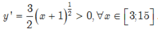
Do đó hàm số đồng biến trên [3; 15]
Hàm số đạt giá trị lớn nhất tại x= 15 và M= y(15)=64.

Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.

f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 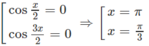
Ta có: f(0) = 0,
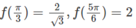
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
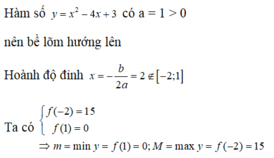
Đáp án D