lim π n 3 n 2 2 n 3 π n − 3 n 2 2 n 2 có g...

PT

Pham Trong Bach

5 tháng 12 2017

lim π n + 3 n + 2 2 n 3 π n − 3 n + 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

5 tháng 12 2017

Đúng(0)

NH

Nguyễn Hải Vân

1 tháng 2 2021

a, lim $\dfrac{\sqrt{n+1}}{1+\sqrt{n}}$

b, lim $\dfrac{1+2+...+n}{n^2+2}$

c, lim $(\sqrt{n^2+n+1}-n)$

d, lim $(\sqrt{3n-1}-\sqrt{2n-1})$

e, lim $(\sqrt[3]{n^3+2n^2}-n)$

g, lim $\dfrac{(2)^{n}+(3)^{n+2}}{4×(3)^{n}+(2)^{n+3}}$

#Hỏi cộng đồng OLM #Toán lớp 11

1

HT

Hoàng Tử Hà

1 tháng 2 2021

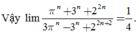
a/ $=\lim\limits\dfrac{\sqrt{\dfrac{n}{n}+\dfrac{1}{n}}}{\dfrac{1}{\sqrt{n}}+\sqrt{\dfrac{n}{n}}}=1$

b/ $1+2+...+n=\dfrac{n\left(n+1\right)}{2}$

$\Rightarrow\lim\limits\dfrac{n\left(n+1\right)}{2n^2+4}=\lim\limits\dfrac{\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}{\dfrac{2n^2}{n^2}+\dfrac{4}{n^2}}=\dfrac{1}{2}$

c/ $=\lim\limits\dfrac{n^2+n+1-n^2}{\sqrt{n^2+n+1}+n}=\lim\limits\dfrac{n+1}{\sqrt{n^2+n+1}+n}=\lim\limits\dfrac{\dfrac{n}{n}+\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{n}{n^2}+\dfrac{1}{n^2}}+\dfrac{n}{n}}=\dfrac{1}{1+1}=\dfrac{1}{2}$

d/ $=\lim\limits\left[\sqrt{n}\left(\sqrt{3-\dfrac{1}{\sqrt{n}}}-\sqrt{2-\dfrac{1}{\sqrt{n}}}\right)\right]=\lim\limits\left[\sqrt{n}\left(\sqrt{3}-\sqrt{2}\right)\right]=+\infty$

e/ $=\lim\limits\dfrac{n^3+2n^2-n-n^3}{\left(\sqrt[3]{n^3+2n^2}\right)^2+n.\sqrt[3]{n^3+2n^2}+n^2}=\lim\limits\dfrac{2n^2-n}{\left(n^3+2n^2\right)^{\dfrac{2}{3}}+n.\left(n^3+2n^2\right)^{\dfrac{1}{3}}+n^2}$

$=\dfrac{2}{1+1+1}=\dfrac{2}{3}$

g/ $=\lim\limits\dfrac{2^n+9.3^n}{4.3^n+8.2^n}=\lim\limits\dfrac{\left(\dfrac{2}{3}\right)^n+9.\left(\dfrac{3}{3}\right)^n}{4.\left(\dfrac{3}{3}\right)^n+8.\left(\dfrac{2}{3}\right)^n}=\dfrac{9}{4}$

Đúng(2)

NH

Nguyễn Hải Vân

1 tháng 2 2021

Mình cảm ơn nhiều nhé❤

Đúng(0)

DT

Đỗ Thị Thanh Huyền

16 tháng 2 2021

tính các giới hạn sau

a) lim (3n^2+n^2-1) b)lim n^3+3n+1/2n-n^3

c) lim -2n^3+3n+1/n-n^2 d) lim(n+ căn n^2-2n

e) lim (2n-3*2n+1) f) (căn 4n^2-n -2n) g) lim (căn n^2+3n-1 - 3^căn n^3-n)

#Hỏi cộng đồng OLM #Toán lớp 11

1

HT

Hoàng Tử Hà

16 tháng 2 2021

Chụp ảnh hoặc sử dụng gõ công thức nhé bạn. Để vầy khó hiểu lắm

undefined

Đúng(1)

DT

Đỗ Thị Thanh Huyền

16 tháng 2 2021

tính các giới hạn sau:a) lim (3n2+n2-1)b)lim $\dfrac{n^3+3n+1}{2n-n^3}$c) lim $\dfrac{-2n^3+3n+1}{n-n^2}$d) lim $\left(n+\sqrt{n^2-2n}\right)$e) lim $\left(2n-3.2^n+1\right)$f) lim $\left(\sqrt{4n^2-n}-2n\right)$g) lim...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 11

3

HT

Hoàng Tử Hà

16 tháng 2 2021

a/ Bạn coi lại đề bài, 3n^2 +n^2 thì bằng 4n^2 luôn chứ ko ai cho đề bài như vậy cả

b/ $\lim\limits\dfrac{\dfrac{n^3}{n^3}+\dfrac{3n}{n^3}+\dfrac{1}{n^3}}{-\dfrac{n^3}{n^3}+\dfrac{2n}{n^3}}=-1$

c/ $=\lim\limits\dfrac{-\dfrac{2n^3}{n^2}+\dfrac{3n}{n^2}+\dfrac{1}{n^2}}{-\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}=\lim\limits\dfrac{-2n}{-1}=+\infty$

d/ $=\lim\limits\left[n\left(1+1\right)\right]=+\infty$

e/ $\lim\limits\left[2^n\left(\dfrac{2n}{2^n}-3+\dfrac{1}{2^n}\right)\right]=\lim\limits\left(-3.2^n\right)=-\infty$

f/ $=\lim\limits\dfrac{4n^2-n-4n^2}{\sqrt{4n^2-n}+2n}=\lim\limits\dfrac{-\dfrac{n}{n}}{\sqrt{\dfrac{4n^2}{n^2}-\dfrac{n}{n^2}}+\dfrac{2n}{n}}=-\dfrac{1}{2+2}=-\dfrac{1}{4}$

g/ $=\lim\limits\dfrac{n^2+3n-1-n^2}{\sqrt{n^2+3n-1}+n}+\lim\limits\dfrac{n^3-n^3+n}{\sqrt[3]{\left(n^3-n\right)^2}+n.\sqrt[3]{n^3-n}+n^2}$

$=\lim\limits\dfrac{\dfrac{3n}{n}-\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{3n}{n^2}-\dfrac{1}{n^2}}+\dfrac{n}{n}}+\lim\limits\dfrac{\dfrac{n}{n^2}}{\dfrac{\sqrt[3]{\left(n^3-n\right)^2}}{n^2}+\dfrac{n\sqrt[3]{n^3-n}}{n^2}+\dfrac{n^2}{n^2}}$

$=\dfrac{3}{2}+0=\dfrac{3}{2}$

Đúng(3)

HQ

Hồng Quang

16 tháng 2 2021

không thích coi rồi sao kh :D

Đúng(1)

DN

Dương Nguyễn

18 tháng 1 2022

1/ lim $\dfrac{\sqrt{n^4-n^2}+3n^2}{1-n^2}$

2/ lim $\dfrac{n\sqrt{n}-n^3}{4n^3+\sqrt{n}}$

3/ lim $\dfrac{3.4^n-1}{2.3^n+4}$

4/ lim $\dfrac{2^{n+1}+4.3^{n-1}}{1-2^{n-1}+3^{n+1}}$

#Hỏi cộng đồng OLM #Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 1 2022

1/...

2/ $=\lim\dfrac{\dfrac{1}{n\sqrt{n}}-1}{4+\dfrac{1}{n^2\sqrt{n}}}=\dfrac{0-1}{4+0}=-\dfrac{1}{4}$ (chia cả tử-mẫu cho $n^3$)

3/ $=\lim\dfrac{3-\left(\dfrac{1}{4}\right)^n}{2.\left(\dfrac{3}{4}\right)^n+4\left(\dfrac{1}{4}\right)^n}=\dfrac{3-0}{2.0+3.0}=\dfrac{3}{0}=+\infty$ (chia tử mẫu cho $4^n$)

4/ $=\lim\dfrac{2.2^n+\dfrac{4}{3}.3^n}{1-\dfrac{1}{2}.2^n+3.3^n}=\lim\dfrac{2.\left(\dfrac{2}{3}\right)^n+\dfrac{4}{3}}{\left(\dfrac{1}{3}\right)^n-\dfrac{1}{2}.\left(\dfrac{2}{3}\right)^n+3}=\dfrac{2.0+\dfrac{4}{3}}{0-\dfrac{1}{2}.0+3}=\dfrac{4}{9}$ (chia tử mẫu cho $3^n$)

Đúng(7)

NN

nguyen ngoc son

24 tháng 11 2023

...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 11 2023

a: $\lim\limits_{n\rightarrow+\infty}\dfrac{n^5+n^2-n+2}{\left(2n^3-1\right)\left(n^2+n+1\right)}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{1+\dfrac{1}{n^3}-\dfrac{1}{n^4}+\dfrac{2}{n^5}}{\left(\dfrac{2n^3}{n^3}-\dfrac{1}{n^3}\right)\left(\dfrac{n^2+n+1}{n^2}\right)}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{1+\dfrac{1}{n^3}-\dfrac{1}{n^4}+\dfrac{2}{n^5}}{\left(2-\dfrac{1}{n^3}\right)\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}\right)}$

$=\dfrac{1}{2\cdot1}=\dfrac{1}{2}$

b: $\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt{n^2-n+2}}{n+2}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{n\sqrt{1-\dfrac{1}{n}+\dfrac{2}{n^2}}}{n\left(1+\dfrac{2}{n}\right)}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt{1-\dfrac{1}{n}+\dfrac{2}{n^2}}}{1+\dfrac{2}{n}}=\dfrac{\sqrt{1-0+0}}{1+0}=\dfrac{1}{1}=1$

c: $\lim\limits_{n\rightarrow+\infty}\dfrac{n-\sqrt[3]{n^2-n^3}}{n^2+n+1}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{\dfrac{n}{n^2}-\dfrac{\sqrt[3]{n^2-n^3}}{n^2}}{1+\dfrac{1}{n}+\dfrac{1}{n^2}}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{\dfrac{1}{n}-\sqrt[3]{\dfrac{1}{n^4}-\dfrac{1}{n^3}}}{1+\dfrac{1}{n}+\dfrac{1}{n^2}}=\dfrac{0}{1}=0$

d: $\lim\limits_{n\rightarrow+\infty}\left(n-\sqrt{n^2+n+1}\right)$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{n^2-n^2-n-1}{n+\sqrt{n^2+n+1}}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{-n-1}{n+\sqrt{n^2+n+1}}$

$=\lim\limits_{n\rightarrow+\infty}\dfrac{-1-\dfrac{1}{n}}{1+\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}}=-\dfrac{1}{1+1}=-\dfrac{1}{2}$

Đúng(2)

TN

Thư Nguyễn Huỳnh Anh

20 tháng 1 2021

...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 1 2021

$a=\lim\sqrt{n^3}\sqrt{\dfrac{1}{n^3}+\dfrac{2}{n^2}-1}=\infty.\left(-1\right)=-\infty$

$b=\lim\left(\sqrt{n^2+2n+3}-n+n-\sqrt[3]{n^2+n^3}\right)$

$=\lim\dfrac{2n+3}{\sqrt{n^2+2n+3}+n}+\lim\dfrac{-n^2}{n^2+n\sqrt[3]{n^2+n^3}+\sqrt[3]{\left(n^2+n^3\right)^2}}$

$=\lim\dfrac{2+\dfrac{3}{n}}{\sqrt{1+\dfrac{2}{n}+\dfrac{3}{n^2}}+1}+\lim\dfrac{-1}{1+\sqrt[3]{\dfrac{1}{n}+1}+\sqrt[3]{\left(\dfrac{1}{n}+1\right)^2}}=\dfrac{2}{2}-\dfrac{1}{3}=\dfrac{2}{3}$

$c=\lim\dfrac{\left(\dfrac{2}{\sqrt{n}}+\dfrac{1}{n}\right)\left(\dfrac{1}{\sqrt{n}}+\dfrac{3}{n}\right)}{\left(1+\dfrac{1}{n}\right)\left(1+\dfrac{2}{n}\right)}=\dfrac{0.0}{1.1}=0$

Đúng(1)

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 1 2021

$d=\lim\dfrac{4-3\left(\dfrac{2}{4}\right)^n}{9.\left(\dfrac{3}{4}\right)^n+\left(\dfrac{2}{4}\right)^n}=\dfrac{4}{0}=+\infty$

$e=\lim\dfrac{7-25\left(\dfrac{5}{7}\right)^n+3.\left(\dfrac{1}{7}\right)^n}{12.\left(\dfrac{6}{7}\right)^n-\left(\dfrac{3}{7}\right)^n+3\left(\dfrac{1}{7}\right)^n}=\dfrac{7}{0}=+\infty$

$f=\lim\dfrac{n^4-4n^6}{n\left(\sqrt{n^4+1}+\sqrt{4n^6+1}\right)}=\lim\dfrac{\dfrac{1}{n^2}-6}{\sqrt{\dfrac{1}{n^6}+\dfrac{1}{n^{10}}}+\sqrt{\dfrac{4}{n^4}+\dfrac{1}{n^{10}}}}=\dfrac{-6}{0}=-\infty$

Đúng(0)

NL

nguyễn linh chi

19 tháng 2 2020

tìm các giới...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

19 tháng 2 2020

a/ $=lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\infty}=0$

b/ $=lim\frac{6n+1}{\sqrt{n^2+5n+1}+\sqrt{n^2-n}}=\frac{6+\frac{1}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{1}{n}}}=\frac{6}{1+1}=3$

c/ $=lim\frac{6n-9}{\sqrt{3n^2+2n-1}+\sqrt{3n^2-4n+8}}=lim\frac{6-\frac{9}{n}}{\sqrt{3+\frac{2}{n}-\frac{1}{n^2}}+\sqrt{3-\frac{4}{n}+\frac{8}{n^2}}}=\frac{6}{\sqrt{3}+\sqrt{3}}=\sqrt{3}$

d/ $=lim\frac{\left(\frac{2}{6}\right)^n+1-4\left(\frac{4}{6}\right)^n}{\left(\frac{3}{6}\right)^n+6}=\frac{1}{6}$

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

19 tháng 2 2020

e/ $=lim\frac{\left(\frac{3}{5}\right)^n-\left(\frac{4}{5}\right)^n+1}{\left(\frac{3}{5}\right)^n+\left(\frac{4}{5}\right)^n-1}=\frac{1}{-1}=-1$

f/ Ta có công thức:

$1+3+...+\left(2n+1\right)^2=\left(n+1\right)^2$

$\Rightarrow lim\frac{1+3+...+2n+1}{3n^2+4}=lim\frac{\left(n+1\right)^2}{3n^2+4}=lim\frac{\left(1+\frac{1}{n}\right)^2}{3+\frac{4}{n^2}}=\frac{1}{3}$

g/ $=lim\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\right)=lim\left(1-\frac{1}{n+1}\right)=1-0=1$

h/ Ta có: $1^2+2^2+...+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

$\Rightarrow lim\frac{n\left(n+1\right)\left(2n+1\right)}{6n\left(n+1\right)\left(n+2\right)}=lim\frac{2n+1}{6n+12}=lim\frac{2+\frac{1}{n}}{6+\frac{12}{n}}=\frac{2}{6}=\frac{1}{3}$

Đúng(0)

NN

nguyen ngoc son

27 tháng 11 2023

tính giới hạn

1.$\lim\limits\left(n^3+4n^2-1\right)$

2.$lim\dfrac{\left(n+1\right)\sqrt{n^2-n+1}}{3n^2+n}$

3.$lim\dfrac{1+2+....+n}{2n^2}$

4.$lim\dfrac{3^n-4.2^{n-1}-10}{7.2^n+4^n}$

#Hỏi cộng đồng OLM #Toán lớp 11

2

AH

Akai Haruma

Giáo viên

27 tháng 11 2023

1.

$\lim (n^3+4n^2-1)=\infty$ khi $n\to \infty$

2.

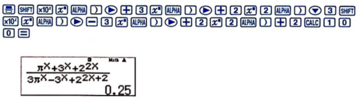
$\lim\limits_{n\to -\infty} \frac{(n+1)\sqrt{n^2-n+1}}{3n^2+n}=\lim\limits_{n\to -\infty}\frac{-\frac{n+1}{n}.\sqrt{\frac{n^2-n+1}{n^2}}}{3+\frac{1}{n}}\\ =\lim\limits_{n\to -\infty}\frac{-(1+\frac{1}{n})\sqrt{1-\frac{1}{n}+\frac{1}{n^2}}}{3+\frac{1}{n}}=\frac{-1}{3}$

$\lim\limits_{n\to +\infty} \frac{(n+1)\sqrt{n^2-n+1}}{3n^2+n}=\lim\limits_{n\to +\infty}\frac{\frac{n+1}{n}.\sqrt{\frac{n^2-n+1}{n^2}}}{3+\frac{1}{n}}\\ =\lim\limits_{n\to +\infty}\frac{(1+\frac{1}{n})\sqrt{1-\frac{1}{n}+\frac{1}{n^2}}}{3+\frac{1}{n}}=\frac{1}{3}$

Đúng(2)

AH

Akai Haruma

Giáo viên

27 tháng 11 2023

3.

$\lim \frac{1+2+...+n}{2n^2}=\lim \frac{n(n+1)}{4n^2}=\lim \frac{n^2+n}{4n^2}\\ =\lim (\frac{1}{4}+\frac{1}{4n})=\frac{1}{4}$

4.

$\lim \frac{3^n-4.2^{n-1}-10}{7.2^n+4^n}=\lim \frac{(\frac{3}{4})^n-(\frac{2}{4})^{n-1}-\frac{10}{4^n}}{7(\frac{2}{4})^n+1}\\ =\lim \frac{(\frac{3}{4})^n-(\frac{1}{2})^{n-1}-\frac{10}{4^n}}{7(\frac{1}{2})^n+1}\\ =\frac{0-0-0}{7.0+1}=0$

Đúng(1)

NV

Nguyễn Văn Trí

11 tháng 1 2023

$1.lim\left(\sqrt[3]{8n^3+4n^2+1}-\sqrt[3]{8n^3-2}\right)$

$2.lim\left(\sqrt[3]{n^3+n^2+1}+\sqrt[3]{8-n^3}\right)$

$3.lim\left(\sqrt[3]{n^3+n^2+2}-n\right)$

#Hỏi cộng đồng OLM #Toán lớp 11

0

JE

Julian Edward

13 tháng 1 2021

Tính:

A= $lim\dfrac{n+1}{n^2+2n}$

B= $lim\left(-2n^3+n^2+2\right)$

C= $lim\dfrac{\sqrt{9n^2-n-1}}{4n-2}$

D= $lim\dfrac{3^n+5.4^n}{4^n+2^n}$

#Hỏi cộng đồng OLM #Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

13 tháng 1 2021

$a=\lim\dfrac{\dfrac{1}{n}+\dfrac{1}{n^2}}{1+\dfrac{2}{n}}=\dfrac{0}{1}=0$

$b=\lim n^3\left(-2+\dfrac{1}{n}+\dfrac{2}{n^3}\right)=+\infty.\left(-2\right)=-\infty$

$c=\lim\dfrac{\sqrt{9-\dfrac{1}{n}-\dfrac{1}{n^2}}}{4-\dfrac{2}{n}}=\dfrac{\sqrt{9}}{4}=\dfrac{3}{4}$

$d=\lim\dfrac{\left(\dfrac{3}{4}\right)^n+5}{1+\left(\dfrac{2}{4}\right)^n}=\dfrac{5}{1}=5$

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP