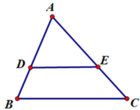
Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
A. 30
B. 36
C. 25
D. 27
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 4 2018
Vì DE // BC, theo định lý Ta-lét ta có A D D B = A E E C ⇔ 12 18 = A E 30
=> EA = 30.12 18 = 20 cm
Nên AC = AE + EC = 50 cm
Đáp án: C
6 tháng 9 2023
a) Ta có :
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\)
\(S_{ADE}=\dfrac{1}{2}AD.AE.sinA\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\dfrac{AB.AC}{AD.AE}=\dfrac{48.64}{32.24}=4\)
\(\Rightarrow S_{ABC}=4S_{ADE}\)
b) Xét \(\Delta ABC\) ta có :
\(p=\left(AB+AC+BC\right):2=\left(48+36+64\right):2=74\left(cm\right)\)
Theo công thức Heron :
\(S_{ABC}=\sqrt[]{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74\left(74-48\right)\left(74-64\right)\left(74-36\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74.26.10.38}=4\sqrt[]{5.13.19.37}=4\sqrt[]{45695}\left(cm^2\right)\)
\(\Rightarrow S_{ADE}=\dfrac{S_{ABC}}{4}=\dfrac{4\sqrt[]{45695}}{4}=\sqrt[]{45695}\left(cm^2\right)\)
Xét \(\Delta ADE\) ta có :
Đặt \(DE=x\left(x>0\right)\)
\(p=\dfrac{\left(AD+AE+x\right)}{2}=\dfrac{\left(32+24+x\right)}{2}=\dfrac{56+x}{2}=28+\dfrac{x}{2}\left(cm\right)\)
\(S_{ADE}=\sqrt[]{p\left(p-AD\right)\left(p-AE\right)\left(p-DE\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(28+\dfrac{x}{2}-32\right)\left(28+\dfrac{x}{2}-24\right)\left(28+\dfrac{x}{2}-x\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)}\)
\(\Rightarrow S^2_{ADE}=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow45695=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow5.13.19.37=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\left(1\right)\)
Ta thấy khi \(x=18\) thì vế phải có :
\(\left\{{}\begin{matrix}\dfrac{x}{2}-4=5\\\dfrac{x}{2}+4=13\\28-\dfrac{x}{2}=19\\28+\dfrac{x}{2}=37\end{matrix}\right.\) \(\Rightarrow x=18\) pt (1) thỏa
Vậy \(DE=18\left(cm\right)\)
13 tháng 6 2015
Hai lần tổng độ dài 3 cạnh là :
18 + 22 + 36 =76
Tổng độ dài 3 canh là :
76 : 2 = 38
Độ dài cạnh CA là :
38 - 18 = 20
Độ dài cạnh AB là :
38 - 22 = 16
Độ dài cạnh BC là :
38 - 36 = 2
Đáp số :
Vì DE // BC, theo định lý Ta-lét ta có
A D D B = A E E C ⇔ A D 18 = 12 36 − 12 ⇔ A D 18 = 12 24
=> AD = 18.12 24 = 9 cm
Nên AB = AD + DB = 9 + 18 = 27 cm
Đáp án: D