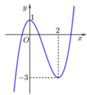
Cho hàm số có đồ thị như hình bên. Hỏi phương trình có bao nhiêu nghiệm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.

Đáp án B
![]()
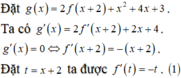
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
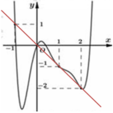
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




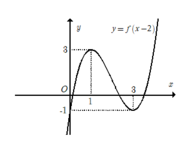
+ Trước tiên tịnh tiến đồ thị sang phải 2 đơn vị để được đồ thị hàm số y= f(x-2) .
Tiếp theo giữ phần đồ thị phía bên phải đường thẳng x= 2, xóa bỏ phần đồ thị phía bên trái đường thẳng x= 2.
Cuối cùng lấy đối xứng phần đồ thị vừa giữ lại ở trên qua đường thẳng x= 2. Ta được toàn bộ phần đồ thị của hàm số
y = f(|x-2|) (hĩnh vẽ bên dưới)
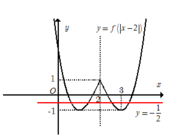
Dựa vào đồ thị hàm số y = f(|x -2|) , ta thấy đường thẳng y= -1/2 cắt đồ thị hàm số y = f(|x-2|) tại 4 điểm phân biệt khi và chỉ khi phương trình f(|x-2|) = -1/2 có 4 nghiệm phân biệt.
Chọn D.

Chọn D.
Phương pháp: Dựa vào đồ thị hàm số.
Cách giải: Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y = -3 nên số nghiệm là 3.
Đáp án D