\(\Delta\)ABC đều có S=121\(\sqrt{3}\)cm2. Tính độ dài cạnh của \(\Delta\)ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔCAB có KD//AB
nên ΔCDK đồng dạng với ΔCBA
=>\(\dfrac{S_{CDK}}{S_{CBA}}=\left(\dfrac{CD}{CB}\right)^2\)
=>\(S_{CBA}=16:\dfrac{CD^2}{CB^2}=16\cdot\dfrac{CB^2}{CD^2}\)
Xét ΔBED và ΔBAC có
góc BED=góc BAC
góc B chung
=>ΔBED đồng dạng với ΔBAC
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{BD}{BC}\right)^2\)
=>\(S_{ABC}=9\cdot\dfrac{BC^2}{BD^2}=16\cdot\dfrac{BC^2}{CD^2}\)
=>3/BD=4/CD
=>BC=7/3BD
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{3}{7}\right)^2=\dfrac{9}{49}\)
=>\(S_{BAC}=49\left(cm^2\right)\)

A B C M 2cm 2cm 2cm
a) Vì AM là trung tuyến của \(\Delta ABC\)tại A \(\Rightarrow MB=MC\)
Vì \(\Delta ABM\)là tam giác đều có cạnh là 2cm\(\Rightarrow AB=AM=BM=2cm\)
Do đó độ dài cạnh BC là : \(2+2=4cm\)
Áp dụng định lý Py-ta-go trong tam giác vuông ABC ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AC=\sqrt{12}\left(cm\right)\)
b) Diện tích \(\Delta ABC\)là : \(\frac{1}{2}\left(AB.AC\right)=\frac{2.\sqrt{12}}{2}=\sqrt{12}\left(cm^2\right)\)

a)Vì M là trung điểm BC (gt)
=> MB = MC
Xét △AMB và △AMC có
AB=AC (gt)
AM : cạnh chung
MB=MC (cmt)
=> △AMB = △AMC (c.c.c)
b) Vì △ABC cân tại A (AB=AC) có AM là trung tuyến
=> AM là đường cao
=> AM ⊥ BC

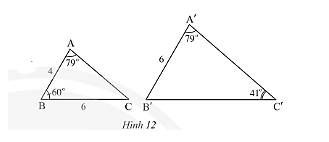
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).

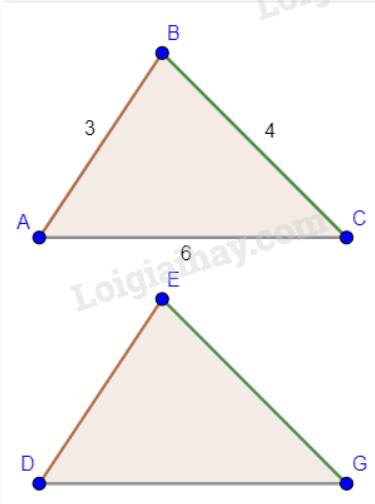
\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.
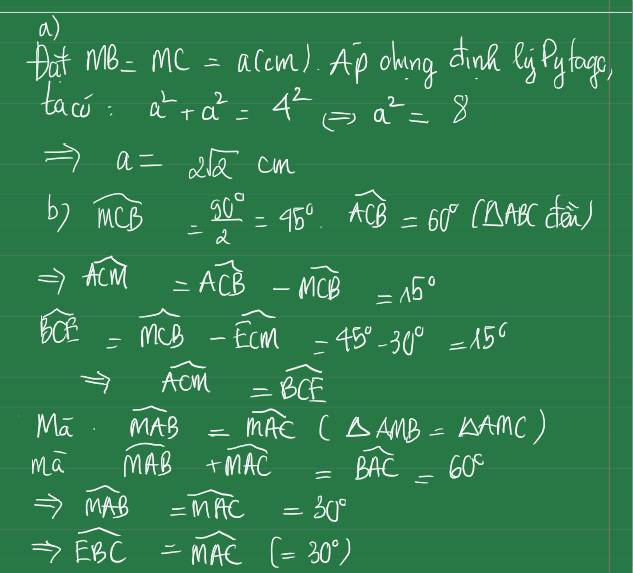
ta có Sabcd=(a^2. căn 3):4
=> 121.căn 3=(a^2.căn 3):4
=> a^2. căn 3=121.căn3.4
=> a^2=121.căn 3.4: căn 3
=> a^2=484
=> a=22,a=-22