U1=3
U2=5
U15=3U14-U13
Tính U15
Theo công thức Un=3un-Un-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 11 2018
Ta có:
u 2 = u 1 + 2 = 3 + 2 = 5.
u 3 = u 2 + 2 = 5 + 2 = 7.
u 4 = u 3 + 2 = 7 + 2 = 9.
u 5 = u 4 + 2 = 9 + 2 = 11.
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát u n có dạng:
u n = 2 n + 1 ∀ n ≥ 1 ∗
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.
Với n =1 ; u 1 = 2 . 1 + 1 = 3 (đúng). Vậy (*) đúng với n =1
Giả sử (*) đúng với n =k. Có nghĩa ta có: u k = 2 k + 1 (2)
Ta cần chứng minh (*) đúng với n = k+1 - có nghĩa là ta phải chứng minh:
u k + 1 = 2(k+1)+1= 2k + 3
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = u k +2 = 2k +1 +2 = 2k + 3
Vậy (*) đúng khi n = k+1 .
Kết luận (*) đúng với mọi số nguyên dương n.
Đáp án B
CM
26 tháng 12 2018
Chọn B
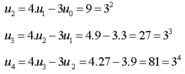
Dự đoán ta được u n = 3 n
Lại có 3 n + 1 = 4.3 n − 3.3 n − 1
Vậy u n = 3 n
CM
25 tháng 6 2018
Ta có
u n + 1 = u n + u n - 1 ⇒ u 3 = u 2 + u 1 = 3 + 2 > 3 = u 2
⇒ u 4 = u 3 + u 2 > u 2 + u 1 = u 3
Theo nguyên lý quy nạp ta có 
là dãy tăng
u n + 1 = u n + u n - 1 < 2 u n + 1 ⇔ u n + 1 2 < 4 u n + 1 ⇔ 0 < u n + 1 < 4
Vậy u n tăng và bị chặn.
Đáp án cần chọn là A
CM
25 tháng 8 2019
Chọn C.
Phương pháp:
SHTQ của cấp số cộng có số hạng đầu u1
công sai d là u n = u 1 + ( n - 1 ) d
Cách giải:
Do u n + 1 = u n + 5 2 , n ≥ 1
⇒ Dãy số trên là 1 CSC có u 1 = - 3 , d = 5 2
CM
3 tháng 3 2019
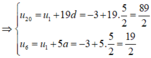
Để chứng tỏ ( u n ) không phải là cấp số cộng, ta chỉ cần chỉ ra, chẳng hạn u 3 − u 2 ≠ u 2 − u 1 là đủ.
