Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = sin(2x + ) (*)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2

a: \(x^2+\left(2m+1\right)x+m^2-3=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\left(m^2-3\right)\)
\(=4m^2+4m+1-4m^2+12=4m+13\)
Để phương trình có nghiệm kép thì 4m+13=0
=>\(m=-\dfrac{13}{4}\)
Thay m=-13/4 vào phương trình, ta được:
\(x^2+\left(2\cdot\dfrac{-13}{4}+1\right)x+\left(-\dfrac{13}{4}\right)^2-3=0\)
=>\(x^2-\dfrac{11}{2}x+\dfrac{121}{16}=0\)
=>\(\left(x-\dfrac{11}{4}\right)^2=0\)
=>x-11/4=0
=>x=11/4
b: TH1: m=2
Phương trình sẽ trở thành \(\left(2+1\right)x+2-3=0\)
=>3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)
=>Khi m=2 thì phương trình có nghiệm kép là x=1/3
TH2: m<>2
\(\text{Δ}=\left(m+1\right)^2-4\left(m-2\right)\left(m-3\right)\)
\(=m^2+2m+1-4\left(m^2-5m+6\right)\)
\(=m^2+2m+1-4m^2+20m-24\)
\(=-3m^2+22m-23\)
Để phương trình có nghiệm kép thì Δ=0
=>\(-3m^2+22m-23=0\)
=>\(m=\dfrac{11\pm2\sqrt{13}}{3}\)
*Khi \(m=\dfrac{11+2\sqrt{13}}{3}\) thì \(x_1+x_2=\dfrac{-m-1}{m-2}=\dfrac{2-2\sqrt{13}}{3}\)
=>\(x_1=x_2=\dfrac{1-\sqrt{13}}{3}\)
*Khi \(m=\dfrac{11-2\sqrt{13}}{3}\) thì \(x_1+x_2=\dfrac{-m-1}{m-2}=\dfrac{2+2\sqrt{13}}{3}\)
=>\(x_1=x_2=\dfrac{1+\sqrt{13}}{3}\)
c: TH1: m=0
Phương trình sẽ trở thành
\(0x^2-\left(1-2\cdot0\right)x+0=0\)
=>-x=0
=>x=0
=>Nhận
TH2: m<>0
\(\text{Δ}=\left(-1+2m\right)^2-4\cdot m\cdot m\)
\(=4m^2-4m+1-4m^2=-4m+1\)
Để phương trình có nghiệm kép thì -4m+1=0
=>-4m=-1
=>\(m=\dfrac{1}{4}\)
Khi m=1/4 thì \(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left[-1+2m\right]}{m}=\dfrac{-2m+1}{m}\)
=>\(x_1+x_2=\dfrac{-2\cdot\dfrac{1}{4}+1}{\dfrac{1}{4}}=\dfrac{-\dfrac{1}{2}+1}{\dfrac{1}{4}}=\dfrac{1}{2}:\dfrac{1}{4}=2\)
=>\(x_1=x_2=\dfrac{2}{2}=1\)

Do pt có nghiệm \(x=1\) nên \(a+b+c=0\Rightarrow1-2m+m-4=0\)
\(\Rightarrow m=-3\)
Giá trị của nghiệm còn lại là: \(x_2=\dfrac{c}{a}=\dfrac{m-4}{1}=-7\)

a.
Khi \(m=2\) pt trở thành:
\(2x+3=0\Rightarrow x=-\dfrac{3}{2}\)
b.
Để pt có nghiệm \(x=-1\)
\(\Rightarrow\left(m^2-m\right).\left(-1\right)+m^2-1=0\)
\(\Leftrightarrow-m^2+m+m^2-1=0\)
\(\Leftrightarrow m-1=0\)
\(\Leftrightarrow m=1\)
c.
Pt tương đương:
\(\left(m^2-m\right)x=-\left(m^2-1\right)\)
\(\Leftrightarrow m\left(m-1\right)x=-\left(m-1\right)\left(m+1\right)\)
Pt vô nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow m=0\)
\(\Rightarrow\) pt có nghiệm khi \(m\ne0\)
Pt có vô số nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)=0\end{matrix}\right.\) \(\Leftrightarrow m=1\)
Lời giải:
a. Khi $m=2$ thì pt trở thành:
$2x+3=0\Leftrightarrow x=-\frac{3}{2}$
b. Để pt có nghiệm $x=-1$ thì:
$(m^2-m).(-1)+m^2-1=0$
$\Leftrightarrow m-1=0\Leftrightarrow m=1$
c.
PT $\Leftrightarrow (m^2-m)x=1-m^2$
Để pt vô nghiệm thì: \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-1)=0\\ (1-m)(1+m)\neq 0\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
PT có vô số nghiệm khi \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2= 0\end{matrix}\right.\Leftrightarrow m=1\)
Để PT có nghiệm thì: $m\neq 0$

Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
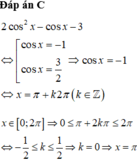
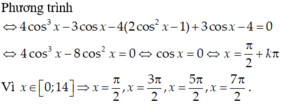
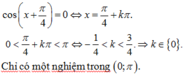
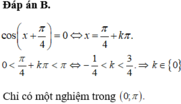
Đáp án B