số nguyên x thỏa mãn - (x - 33) + 92 = 239 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
3 tháng 1 2016
x+(-47)=-33-35
x+(-47)=-33+(-35)
x+(-47)=-68
x =-68-(-47)
x =-68+47
x =-21
Vậy x=-21
Tick nha
CM
23 tháng 9 2018
x + 4 5 − x + 5 < x + 3 3 − x − 2 2
Û 6(x + 4) - 30x + 150 < 10(x + 3) - 15(x - 2)
Û 6x + 24 - 30x + 150 < 10x + 30 - 15x + 30
Û 6x - 30x - 10x + 15x < 30 + 30 - 24 - 150
Û -19x < -114
Û x > 6
Vậy S = { x | x > 6 }
Nghiệm nguyên nhỏ nhất là x = 7.
Đáp án cần chọn là: A
LN
2
KV
22 tháng 12 2023
-10 < x ≤ 13
⇒ x ∈ {-9; -8; -7; ...; 7; 8; 9; 10; 11; 12; 13}
Tổng của chúng là:
-9 + (-8) + (-7) + ... + 7 + 8 + 9 + 10 + 11 + 12 + 13
= 10 + 11 + 12 + 13
= 46
Chọn D
NB
9
29 tháng 12 2016
/x-22/-33=-20
/x-22/=-20+30
/x-22/=10
vậy x - 22 =10 hoặc x-22=-10
x=22+10 x=22+(-10)
x=32 x=12
vậy x=32 hoặc x =12
S
29 tháng 12 2016
\(\left|x-22\right|-33=-20\)
\(\Rightarrow\left|x-22\right|=\left(-20\right)+33\)
\(\Rightarrow\left|x-22\right|=13\)
\(\Rightarrow\orbr{\begin{cases}x-22=13\\-\left(x-22\right)=13\end{cases}\Rightarrow\orbr{\begin{cases}x=35\\-x+22=13\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}x=35\\x=9\end{cases}}\)
MN
Có bao nhiêu số nguyên y sao cho tồn tại x∈ (\(\dfrac{1}{2}\) ;8) thỏa mãn 92\(x^2\)+xy= (1+xy).915x
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)
Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)
Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)
Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)
Do đó:
\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)
\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)
\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)
DT
2
S
4 tháng 5 2023
Gợi ý:
\(2xy+14x+y=33\)
\(\Rightarrow2x\left(y+7\right)+y+7=33+7\)
\(\Rightarrow\left(2x+1\right)\left(y+7\right)=40\)
\(\Rightarrow\left(2x+1;y+7\right)\inƯ\left(40\right)=\left\{\pm1;\pm2;\pm4;\pm5;\pm8;\pm10;\pm20;\pm40\right\}\)
Đến đây thì bạn làm tiếp nhé!
VH
17 giờ trước (19:21)
Nhóm các hạng tử có chứa 𝑥 x và 𝑦 y: 2 𝑥 𝑦 + 14 𝑥 + 𝑦 = 33 2xy+14x+y=33 Nhóm các hạng tử có chứa 𝑥 x và 𝑦 y: 2 𝑥 ( 𝑦 + 7 ) + 𝑦 = 33 2x(y+7)+y=33 Biến đổi phương trình: 2 𝑥 ( 𝑦 + 7 ) + 𝑦 = 33 2x(y+7)+y=33 Thêm 7 vào cả hai vế: 2 𝑥 ( 𝑦 + 7 ) + ( 𝑦 + 7 ) = 40 2x(y+7)+(y+7)=40 Nhân vế trái: ( 𝑦 + 7 ) ( 2 𝑥 + 1 ) = 40 (y+7)(2x+1)=40 Tìm các cặp số nguyên 𝑥 x và 𝑦 y thỏa mãn: Ta xét các ước của 40: ± 1 , ± 2 , ± 4 , ± 5 , ± 8 , ± 10 , ± 20 , ± 40 ±1,±2,±4,±5,±8,±10,±20,±40. Vì 2 𝑥 + 1 2x+1 là số lẻ, nên 𝑦 + 7 y+7 phải là một trong các ước lẻ của 40: ± 1 , ± 5 ±1,±5. Từ đó, ta có các trường hợp sau: Trường hợp 1: 𝑦 + 7 = 1 y+7=1 và 2 𝑥 + 1 = 40 2x+1=40 Giải hệ: 𝑦 = − 6 , 𝑥 = 19 y=−6,x=19 Trường hợp 2: 𝑦 + 7 = − 1 y+7=−1 và 2 𝑥 + 1 = − 40 2x+1=−40 Giải hệ: 𝑦 = − 8 , 𝑥 = − 21 y=−8,x=−21 Trường hợp 3: 𝑦 + 7 = 5 y+7=5 và 2 𝑥 + 1 = 8 2x+1=8 Giải hệ: 𝑦 = − 2 , 𝑥 = 3 y=−2,x=3 Trường hợp 4: 𝑦 + 7 = − 5 y+7=−5 và 2 𝑥 + 1 = − 8 2x+1=−8 Giải hệ: 𝑦 = − 12 , 𝑥 = − 9 y=−12,x=−9 Kết luận: Các cặp số nguyên 𝑥 x và 𝑦 y thỏa mãn phương trình là: ( 𝑥 , 𝑦 ) = ( 19 , − 6 ) , ( − 21 , − 8 ) , ( 3 , − 2 ) , ( − 9 , − 12 ) (x,y)=(19,−6),(−21,−8),(3,−2),(−9,−12) Vậy, các nghiệm của phương trình là ( 𝑥 , 𝑦 ) = ( 19 , − 6 ) , ( − 21 , − 8 ) , ( 3 , − 2 ) , ( − 9 , − 12 ) (x,y)=(19,−6),(−21,−8),(3,−2),(−9,−12).
L
1
9 tháng 3 2023
2y-14x+y=33
=>3y-14x=33
=>3y=14x+33
=>y=14/3x+11
=>x chia hết cho 3 và y=14/3x+11
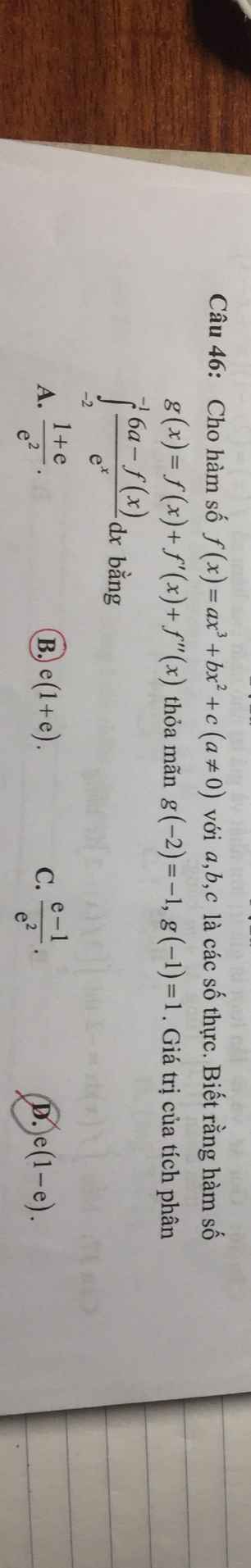
-(x-33)+92= 239
<=> -x+33 +92 =239
<=> -x =114
<=> x= -114
bỏ ngoăc phải đổi dấu nha e
x - 33 = 239 - 92
x - 33 = 147
x = 147 + 33
x = 180