tính tổng A= 1 + 3 + 32 + 33 + ......+ 329 + 330
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
13 tháng 8 2018
1.Quy đồng mẫu số 2 phân số :
3/4 = x/24 bằng :
12/24 = x/24
Vậy x = 12.
2 .
Dãy trên có số số hạng là :
( 330 - 4 ) : 1 + 1 = 327
Dãy số trên có tổng là :
( 330 + 4 ) x 327 : 2 = 54609
Đáp số : 54609
T
13 tháng 8 2018
Bài 1 : Tìm x biết :
3/4 = x/24
<=> 4 . x = 3 . 24
<=> 4 . x = 72
<=> x = 72 : 4
<=> x = 18
Vậy x = 18
Bài 2 : Tính tổng biết :
4 + 5 + 6 + ... + 329 + 330
Số số hạng của dãy trên là :
( 330 - 4 ) : 1 + 1 = 327 ( số hạng )
Tổng của dãy trên là :
( 330 + 4 ) × 327 : 2 = 54 609
=> 4 + 5 + 5 + ... + 329 + 330 = 54 609
ND
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 11 2023
A = 3 + 32 + 33 + ... + 330
3.A = 32 + 33 + 34 + ... + 331
3A - A = 32 + 33 + 34 +... + 331 - (3 + 32 + 33 + ... + 330)
2A = 32 + 33 + 34 + .... + 331 - 3 - 32 - 33 -...- 330
2A = 331 - 3
331 = (34)7.33 - 3 = \(\overline{...1}\)7.27 - 3 = \(\overline{...7}\) - 3 = \(\overline{...4}\)
2.A = \(\overline{...4}\) ⇒ A = \(\overline{..2}\); \(\overline{...7}\) (1)
A = 3 + 32 + ... + 330
A = 31 + 32 + ... + 330
Xét dãy số: 1; 2;...; 30 dãy số này có số số hạng là 30
Vậy A có 30 hạng tử. Vì mỗi hạng tử của A là một số lẻ nên A là tổng của 30 số lẻ vậy A là số chẵn (2)
Kết hợp (1) và (2) ta có: A = \(\overline{..2}\)
Kết luận chữ số hàng đơn vị của A = 3 + 32 +...+ 330 là 2
CM
22 tháng 6 2017
A = 1 + 3 + 3 2 + 3 3 + . . . + 3 30
3 A = 3 + 3 2 + 3 3 + . . . + 3 30 + 3 31
2A = 3A – A = ( 3 + 3 2 + 3 3 + . . . + 3 30 + 3 31 ) – ( 1 + 3 + 3 2 + 3 3 + . . . + 3 30 )
2A = 3 31 - 1
A = 3 31 - 1 2
Ta có 3 1 = 3 ; 3 3 = 9 ; 3 3 = 27 ; 3 4 = 81 ; 3 5 = 243
với n ≥ 0 thì 3 4 n + 3 có chữ số tận cùng là 7.Vì 31 = 4.7 + 3 nên 3 31 có chữ số tận cùng là 7. Do đó 3 31 - 1 2 có chữ số tận cùng là 3. Mà không có số nào bình phương lên có chữ số tận cùng là 3 nên A không là số chính phương.
Tìm chữ số tận cùng của A, từ đó suy ra A không phải số chính phương
TN
2
26 tháng 12 2022
a) A=3+32+33+34+35+36+....+328+329+330A=3+32+33+34+35+36+....+328+329+330
⇔A=(3+32+33)+(34+35+36)+....+(328+329+330)⇔A=(3+32+33)+(34+35+36)+....+(328+329+330)
⇔A=3(1+3+32)+34(1+3+32)+....+328(1+3+32)⇔A=3(1+3+32)+34(1+3+32)+....+328(1+3+32)
⇔A=3.13+34.13+....+328.13⇔A=3.13+34.13+....+328.13
⇔A=13(3+34+....+328)⋮13(dpcm)⇔A=13(3+34+....+328)⋮13(dpcm)
b) A=3+32+33+34+35+36+....+325+326+327+328+329+330A=3+32+33+34+35+36+....+325+326+327+328+329+330
⇔A=(3+32+33+34+35+36)+....+(325+326+327+328+329+330)⇔A=(3+32+33+34+35+36)+....+(325+326+327+328+329+330)
⇔A=3(1+3+32+33+34+35)+....+325(1+3+32+33+34+35)⇔A=3(1+3+32+33+34+35)+....+325(1+3+32+33+34+35)
⇔A=3.364+....+325.364⇔A=3.364+....+325.364
⇔A=364(3+35+310+....+325)⇔A=364(3+35+310+....+325)
⇔A=52.7(3+35+310+....+325)⋮52(dpcm)
13 tháng 6 2019
Ta có: 3A = 3.(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−1
⇒ A = 3101−1
2
Vậy A = 3101−1
2
PT
1
TV
1
S
29 tháng 12 2020
S = 1 + 3 + 32 + 33 +... + 32014
3S = 3 + 32 + 33 + 34 + ... + 32015
3S - S = ( 3 + 32 + 33 + 34 + ... + 32015) - (1 + 3 + 32 + 33 +... + 32014)
2S = 32015 - 1
S = \(\dfrac{3^{2015}-1}{2}\)
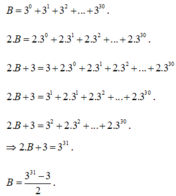
=>3A=3+3^2+3^3+3^4+...+3^30+3^31
=>3A-A=(3+3^2+3^3+3^4+...+3^30+3^31)-(1+3+3^2+3^3+...+3^29+3^30)
=>2A=3^31-1
=>A=(3^31-1)/2
Tick nhé
A=1+3+3^2+3^3+.........+3^29+3^30
3A=3+3^2+3^3+3^4+........+3^30+3^31
3A-A=3^31-1
2A=3^31-1
A=(3^31-1):2