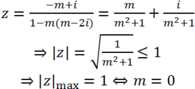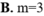tìm Max M=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2020
Ta có: \(2x^2+2x+5=2\left(x^2+x+\dfrac{5}{2}\right)=2\left[x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4}\right]=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{9}{2}\ge\dfrac{9}{2}\forall x\)
=> \(M=\dfrac{1}{2x^2+2x+5}\le\dfrac{1}{\dfrac{9}{2}}=\dfrac{2}{9}\forall x\)
Dấu "=" xảy ra khi \(x=-\dfrac{1}{2}\)
Vậy MaxM=\(\dfrac{2}{9}\) khi x=\(-\dfrac{1}{2}\)
29 tháng 11 2021
\(1,yz\sqrt{x-1}=yz\sqrt{\left(x-1\right)\cdot1}\le yz\cdot\dfrac{x-1+1}{2}=\dfrac{xyz}{2}\)
\(zx\sqrt{y-2}=\dfrac{zx\cdot2\sqrt{2\left(y-2\right)}}{2\sqrt{2}}\le\dfrac{xyz}{2\sqrt{2}}\\ xy\sqrt{z-3}=\dfrac{xy\cdot2\sqrt{3\left(z-3\right)}}{2\sqrt{3}}\le\dfrac{xyz}{2\sqrt{3}}\)
\(\Leftrightarrow M\le\dfrac{\dfrac{xyz}{2}+\dfrac{xyz}{2\sqrt{2}}+\dfrac{xyz}{2\sqrt{3}}}{xyz}=\dfrac{xyz\left(\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\right)}{xyz}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-2=2\\z-3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\\z=6\end{matrix}\right.\)
29 tháng 11 2021
\(2,N^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\\ \Leftrightarrow N^2\le\left(a+b+b+c+c+a\right)\left(1^2+1^2+1^2\right)\\ \Leftrightarrow N^2\le6\left(a+b+c\right)=6\sqrt{2}\\ \Leftrightarrow N\le\sqrt{6\sqrt{2}}\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{\sqrt{2}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 11 2021
\(y'=\dfrac{-2-m}{\left(x-1\right)^2}.e^{\dfrac{2x+m}{x-1}}\)
\(\Rightarrow\) Hàm đơn điệu trên miền xác định
TH1: \(\left\{{}\begin{matrix}-2-m< 0\\y\left(2\right)=e^5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-2\\\dfrac{m+4}{1}=5\end{matrix}\right.\) \(\Rightarrow m=1\)
TH2: \(\left\{{}\begin{matrix}-2-m>0\\y\left(4\right)=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -2\\\dfrac{m+8}{3}=5\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
Vậy \(m=1\)
H3
0
ML
1
19 tháng 12 2016
M=\(\frac{x^2+10x-7}{x^2+2x+1}=\frac{x^2+10x+25-32}{x^2+2x+1}=\frac{\left(x+5\right)^2-32}{\left(x+1\right)^2}\)
\(\Rightarrow\frac{\left(x+5\right)^2-32}{\left(x+1\right)^2}\le-32\)
Vay Max la -32
Mk cx k chắc lắm đâu .