Chứng minh rằng
x - x2 - 2 < 0 với mọi giá trị của x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 4 2018
Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~
PT
1
CM
8 tháng 1 2017
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
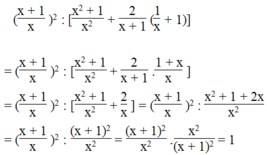
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
NT
1
HV
1
TV
1
30 tháng 10 2021
\(-x^2+8x-19=-\left(x^2-8x+16\right)-3=-\left(x-4\right)^2-3\le-3< 0\)
NA
6 tháng 10 2018
a) Ta có \(2x^2-8x+13=2x^2-8x+8+5\)
\(=2\left(x^2-4x+4\right)+5\)
\(=2\left(x-2\right)^2+5\ge5\forall x\)
6 tháng 10 2018
Giả sử trước khi làm nhé
\(a)\)\(2x^2-8x+13>0\)
\(\Leftrightarrow\)\(4x^2-16x+26>0\)
\(\Leftrightarrow\)\(\left(4x^2-16+16\right)+10>0\)
\(\Leftrightarrow\)\(\left(2x-4\right)^2+10\ge10>0\) ( luôn đúng )
Vậy ...
\(b)\)\(-2+2x-x^2< 0\)
\(\Leftrightarrow\)\(x^2-2x+2>0\)
\(\Leftrightarrow\)\(\left(x^2-2x+1\right)+1>0\)
\(\Leftrightarrow\)\(\left(x-1\right)^2+1\ge1>0\) ( luôn đúng )
Vậy ...
Chúc bạn học tốt ~
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 5 2020
\(\Delta=\left(2m-3\right)^2-4\left(m^2-3m\right)=9>0;\forall m\)
\(\Rightarrow\) Pt đã cho luôn có 2 nghiệm pb
Do \(x_1< x_2\Rightarrow\left\{{}\begin{matrix}x_1=\frac{2m-3-\sqrt{9}}{2}=m-3\\x_2=\frac{2m-3+\sqrt{9}}{2}=m\end{matrix}\right.\)
\(\Rightarrow0< m-3< m< 5\)
\(\Rightarrow3< m< 5\)
12 tháng 5 2023
a: Δ=(2m+2)^2-4(m-6)
=4m^2+8m+4-4m+24
=4m^2+4m+28
=(2m+1)^2+27>0
=>Phương trình luôn có hai nghiệm phân biệt
c: Để (1) có ít nhất 1 nghiệm dương thì
m-6<0 hoặc (2m+2>0 và m-6>0)
=>m>6 hoặc m<6
\(x-x^2-2\)
\(=x-\left(x^2+2\right)\)
Ta có : \(x^2\ge0\forall x\)
\(\Rightarrow x^2+2\ge0\)
mà \(x\le x^2\)
\(\Rightarrow x< x^2+2\)
\(\Rightarrow x-\left(x^2+2\right)< 0\)
\(\Rightarrow x-x^2-2< 0\)
Ta có: \(x-x^2-2=x-x^2-\frac{1}{4}-\frac{7}{4}\)
\(=\left(x-x^2-\frac{1}{4}\right)-\frac{7}{4}=-\left(x^2-x+\frac{1}{4}\right)-\frac{7}{4}\)
\(=-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}\right)-\frac{7}{4}=-\left(x-\frac{1}{2}\right)^2-\frac{7}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)\(\Rightarrow-\left(x-\frac{1}{2}\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-\frac{1}{2}\right)^2-\frac{7}{4}\le-\frac{7}{4}\)\(\forall x\)
\(\Rightarrow x-x^2-2\le-\frac{7}{4}\)\(\forall x\)
hay \(x-x^2-2< 0\)( đpcm )