kết quả rút gọn của biểu thức P = \(\sqrt{\frac{x^2-4x+4}{2-x}}\) ( x \(\ne\)2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
22 tháng 10 2019
a) P = \(\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}+2}\right)\)\(.\)\(\frac{x-4}{\sqrt{4x}}\)
= \(\frac{\sqrt{x}.\left(\sqrt{x}+2\right)+\sqrt{x}.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)\(.\)\(\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{4x}}\)
= \(\frac{x+2\sqrt{x}+x-2\sqrt{x}}{\sqrt{4x}}\)
= \(\frac{2x}{2\sqrt{x}}\)= \(\sqrt{x}\)
b) x = \(3-2\sqrt{2}\)=\(2-2\sqrt{2}+1\)= \(\left(\sqrt{2}-1\right)^2\)
Thay x = \(\left(\sqrt{2}-1\right)^2\) vào P ta được
P = \(\sqrt{\left(\sqrt{2}-1\right)^2}\)= \(\sqrt{2}-1\)
27 tháng 10 2020
\(A=\frac{y}{x}\cdot\sqrt{\frac{x^2}{y^4}}=\frac{y}{x}\cdot\frac{\sqrt{x^2}}{\sqrt{y^4}}=\frac{y}{x}\cdot\frac{\left|x\right|}{\left|y^2\right|}=\frac{y}{x}\cdot\frac{x}{y^2}=\frac{1}{y}\)( x > 0 ; y > 0 )
13 tháng 6 2018
a, \(M=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\) (ĐK : \(\forall x\in R\))
\(=\sqrt{\left(x-2\right)^2}-\sqrt{\left(x+2\right)^2}\)
* Nếu x\(\ge2\Rightarrow M=x-2-x-2=-4\)
*Nếu x<2 => M=2-x-x-2=-2x
b,Để M=2\(\ne-4\)
=>M=-2x
=>-2x=-4
=>x=2
__________________________________________________________________________________________
P=\(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
* Nếu \(x\ge2\Rightarrow P=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
* Nếu x<2 =>P=\(\sqrt{x-1}+1+1-\sqrt{x-1}=2\)
VẬY.......
Tk nha!
S
27 tháng 10 2020
\(A=\frac{x}{y}.\frac{x}{y^2}=\frac{x^2}{y^3}\left(\text{vì }x>0;y< 0\text{ nên: }\frac{x}{y^2}>0\right)\)
27 tháng 10 2020
\(A=\frac{x}{y}\cdot\sqrt{\frac{x^2}{y^4}}=\frac{x}{y}\cdot\frac{\sqrt{x^2}}{\sqrt{y^4}}=\frac{x}{y}\cdot\frac{\left|x\right|}{\left|y^2\right|}=\frac{x}{y}\cdot\frac{x}{y^2}=\frac{x^2}{y^3}\)( x > 0 ; y < 0 )
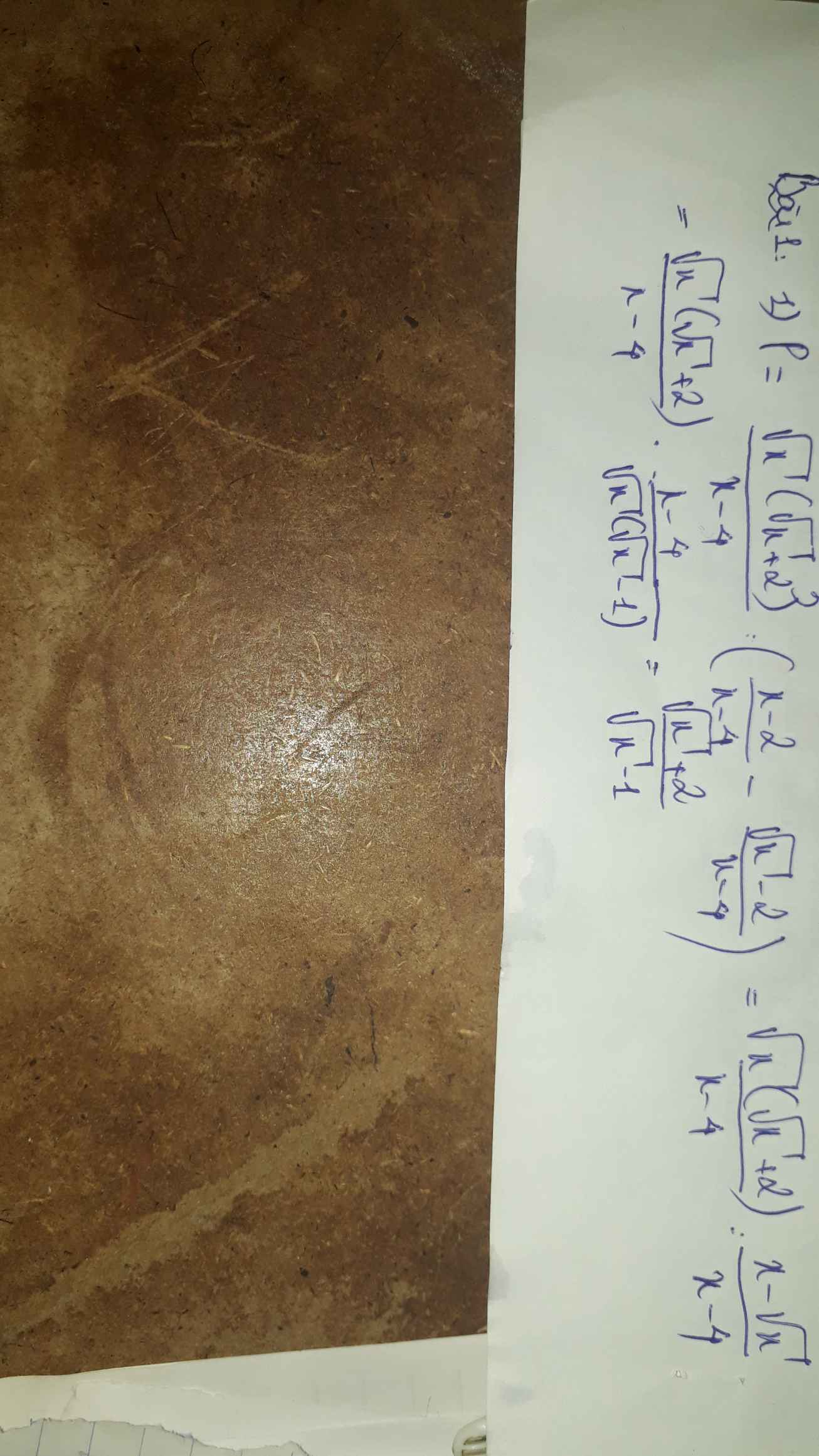
\(P=\sqrt{\frac{x^2-4x+4}{2-x}}\left(x\ne2\right)\)
\(=\sqrt{\frac{\left(2-x\right)^2}{2-x}}\)
\(=\sqrt{2-x}\)
Vì \(x^2-4x+4=\left(x-2\right)^2>0\left(\forall x\right)\) nên để căn thức có nghĩa thì
\(\Rightarrow2-x>0\Rightarrow x< 2\)
Ta có:
\(P=\sqrt{\frac{x^2-4x+4}{2-x}}=\sqrt{\frac{\left(2-x\right)^2}{2-x}}=\sqrt{2-x}\)
Vậy \(P=\sqrt{2-x}\)