Cos13x + sin14x =1
Giải phương trình sau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2020
c/
Đặt \(3cosx-4sinx-6=t\)
Pt trở thành:
\(t^2+2=-3t\Leftrightarrow t^2+3t+2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3cosx-4sinx-6=-1\\3cosx-4sinx-6=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3cosx-4sinx=5\\3cosx-4sinx=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx.\frac{3}{5}-sinx.\frac{4}{5}=1\\cosx.\frac{3}{5}-sinx.\frac{4}{5}=\frac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(x+a\right)=1\\cosx\left(x+a\right)=\frac{4}{5}\end{matrix}\right.\) (với góc \(a\in\left[0;\pi\right]\) sao cho \(cosa=\frac{3}{5}\))
\(\Leftrightarrow\left[{}\begin{matrix}x+a=k2\pi\\x+a=\pm\left(\frac{\pi}{2}-a\right)+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-a+k2\pi\\x=-a\pm\left(\frac{\pi}{2}-a\right)+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2020
a/
\(\Leftrightarrow cosx.\frac{1}{2}-\frac{\sqrt{3}}{2}sinx=cos\left(\frac{\pi}{3}-x\right)\)
\(\Leftrightarrow cosx.cos\left(\frac{\pi}{3}\right)-sinx.sin\left(\frac{\pi}{3}\right)=cos\left(\frac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=cos\left(\frac{\pi}{3}-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=\frac{\pi}{3}-x+k2\pi\\x+\frac{\pi}{3}=-\frac{\pi}{3}+x+k2\pi\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=k\pi\)
b/
\(\Leftrightarrow\sqrt{2}sin\left(5x+\frac{\pi}{4}\right)=\sqrt{2}cos13x\)
\(\Leftrightarrow cos\left(\frac{\pi}{4}-5x\right)=cos13x\)
\(\Leftrightarrow\left[{}\begin{matrix}13x=\frac{\pi}{4}-5x+k2\pi\\13x=-\frac{\pi}{4}+5x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{72}+\frac{k\pi}{9}\\x=-\frac{\pi}{32}+\frac{k\pi}{4}\end{matrix}\right.\)
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
NX
1
12 tháng 5 2023
a: Khi m=2 thì pt sẽ là x^2-6x-3=0
=>\(x=3\pm2\sqrt{3}\)
4 tháng 3 2022
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
4 tháng 3 2022
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
CM
23 tháng 8 2019
4x2 – 1 = (2x + 1)(3x – 5)
⇔ 4x2 – 1 – (2x + 1)(3x – 5) = 0
⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0
⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0
⇔ (2x + 1)(2x – 1 – 3x + 5) = 0
⇔ (2x + 1)(4 – x) = 0
⇔ 2x + 1= 0 hoặc 4 – x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 4 – x = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm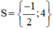 
CM
20 tháng 10 2017
Cách 1:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 - 4(x2 – 2x + 1) = 0
⇔ (x + 1)2 - 22. (x -1)2 = 0
⇔ (x + 1)2 – [ 2(x – 1)]2 =0
⇔ [(x+ 1) + 2( x- 1)]. [(x+ 1) - 2( x- 1)]= 0
⇔ ( x+1+ 2x -2) . (x+1 – 2x + 2) =0
⇔ ( 3x- 1).( 3- x) = 0
⇔ 3x – 1 = 0 hoặc 3 – x= 0
+) 3x – 1 = 0 ⇔ 3x = 1 ⇔ x =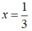 
+) 3 – x = 0 ⇔ x= 3
Vậy tập nghiệm của phương trình đã cho là:
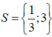
* Cách 2: Ta có:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 - 4(x2 – 2x + 1) = 0
⇔ x2 + 2x +1- 4x2 + 8x – 4 = 0
⇔ - 3x2 + 10x – 3 = 0
⇔ (- 3x2 + 9x) + (x – 3) = 0
⇔ -3x (x – 3)+ ( x- 3) = 0
⇔ ( x- 3). ( - 3x + 1) = 0
⇔ x - 3 = 0 hoặc -3x + 1= 0
+) x - 3 = 0 x = 3
+) - 3x + 1 = 0 - 3x = - 1 ⇔ x =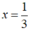 
Vậy tập nghiệm của phương trình đã cho là:
PN
15 tháng 5 2021
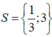
\(\left(x+1\right)^2=4\left(x^2-2x+1\right)\)
\(< =>\left(x+1\right)^2=\left(2x-2\right)^2\)
\(< =>\left(x+1-2x+2\right)\left(x+1+2x-2\right)=0\)
\(< =>\orbr{\begin{cases}-x+3=0\\3x-1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=3\\x=\frac{1}{3}\end{cases}}\)
Lời giải:
Vì $\sin x,\cos x\in [-1;1]$ nên:
$\cos ^{13}x\leq \cos ^2x; \sin ^{14}x\leq \sin ^2x$
$\Rightarrow \cos ^{13}x+\sin ^{14}x\leq \cos ^2x+\sin ^2x$
$\Leftrightarrow \cos ^{13}x+\sin ^{14}x\leq 1$
Dấu "=" xảy ra khi \(\left\{\begin{matrix} \cos ^{13}x=\cos ^2x\\ \sin ^{14}x=\sin ^2x\end{matrix}\right.\)
$\Leftrightarrow x=2k\pi$ hoặc $x=k\pi -\frac{\pi}{2}$ với $k$ nguyên.