Cho tam giác ABC. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC,CA,AB. C/m rằng \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{15^2}+\dfrac{1}{20^2}=\dfrac{625}{90000}\)
\(\Leftrightarrow AH=12\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=15^2-12^2=81\)
hay BH=9(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)
hay CH=16(cm)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC\(\sim\)ΔABC(g-g)
d) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)
\(\widehat{AEH}=90^0\)
\(\widehat{AFH}=90^0\)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
mk cần phần C và D bn có thể diễn giải chi tiết được không

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

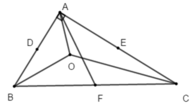
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc CB

a) Có A là hình chiếu của C trên đoạn A
CB là dường xiên của đoạn AB
Suy ra CB lớn hơn AC
Xét Tam giác ABC có
AB nhỏ hơn AC nhỏ hơn CB
Suy ra góc C nhỏ hơn góc B nhỏ hơn góc A (quan hệ giữa góc và cạnh đới diện)
b)CÓ BI là p/g (gt)
Suuy ra góc DBI = góc ABI
Xét tam giác AIB và tam giác DIB có
IB chung
góc DBI = góc ABI (cmt)
AB = BD (gt)
Suy ra tam giác BAI = tam giác BDI (cgc)
Suy ra góc BAI = góc IDB (2 góc tương ứng)
mà góc BAI = 90 độ (tam giác ABC vuông tại A)
Suy ra góc IDB = 90 độ
Suy ra ID vuông góc với BC (định nghĩa)
Đợi mình nghĩ ra câu C

1 2 1 1 2 1 2 A M N B C
a,Xét tam giác ABN và tam giác ACM có :
AM=AN (gt)
Góc A chung
AB=AC(gt)
=> tam giác ABN = tam giác ACM (c-g-c)
b,theo câu a =>AMC^=ANB^(1)
Ta có : AM=AN =>tam giác AMN cân tại A => AMN^=ANM^(2)
Từ 1 và 2 =>MNI^=NMI^(3)
Vì B1^=C1^
B^=C^
=>B^-B1^=C-C1^
=>C2^=B2^(4)
Mặt khác : I1^=I2^(đối đỉnh) (5)
Từ 3 ; 4 và 5 => MNI^+NMI^+I1^=180*=I2^+B2^+C2^(tổng 3 góc của 1 tam giác )
=> MNI^+NMI^ / 2 = B2^+C2^ / 2
=> B2^=MNI^
Vì 2 góc này ở vị trí sole trong và bằng nhau
=> MN // BC

Giải:
a) Diện tích tam giác ABC = 1/2 x AH x BC
Diện tích tam giác ABE = 1/2 x AH x BE
= 1/2 x AH x 2/3 BC
= 1/2 x AH x BC x 2/3
= Diện tích tam giác ABC x 2/3
Vậy: Diện tích tam giác ABE = 2/3 diện tích tam giác ABC.
b) Vì chiều cao DE có D là trung điểm nên Diện tích tam giác ABE = 2 lần diện tích tam giác BDE
= 12 x 2
= 24
Diện tích tam giác ABC = 24 : 2/3
= 36
c) Diện tích hình tứ giác ADEC là: 36 - 24 = 12 ( cm vuông)
Đáp số: ...........................
\(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)+\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)+\frac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\frac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)+\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)=\overrightarrow{0}\)