Tìm GTNN của các hàm số LG: y= 4sin3x + cos2x- cos6x +6=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x
= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x
Do đó : y' = -6cos5xsinx.

\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
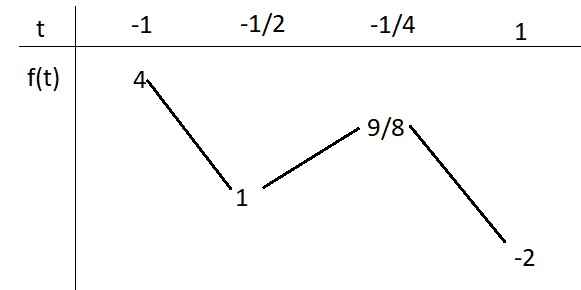
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)

Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)

\(y=sin^3x+2sin^2x+sinx-2\)
đặt \(t=sinx\) với \(t\in\left[-1;1\right]\)
pt \(\Leftrightarrow\)\(y=t^3+2t^2+t-2\)
\(y'=3t^2+4t+1\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{3}\end{matrix}\right.\)
| x | -1 -1/3 1 |
| y' | 0 - 0 + |
| y | -2 - -58/27 + 2 |
vậy GTLN của y = 2 với t=1 \(\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
GTNN của y=-58/27 với \(t=-\dfrac{1}{3}\Leftrightarrow sinx=-\dfrac{1}{3}\Leftrightarrow x=sin^{-1}\left(-\dfrac{1}{3}\right)\)

\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)
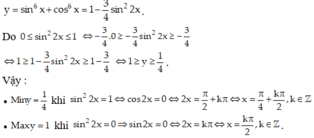
\(y=4sin3x+2cos^2x-1-\left(1-2sin^23x\right)+6\)
\(y=2sin^23x+4sin3x+2cos^2x+4\)
\(y=2\left(sin3x+1\right)^2+2cos^2x+2\ge2\)
\(y_{min}=2\) khi \(x=\frac{\pi}{2}+k2\pi\)