tìm a sao cho
[a;a+12] \(\subset\) (−∞;5) ∪ (−3;∞)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
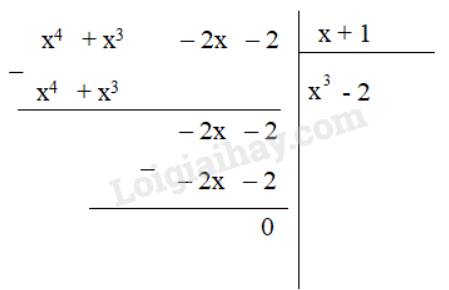
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
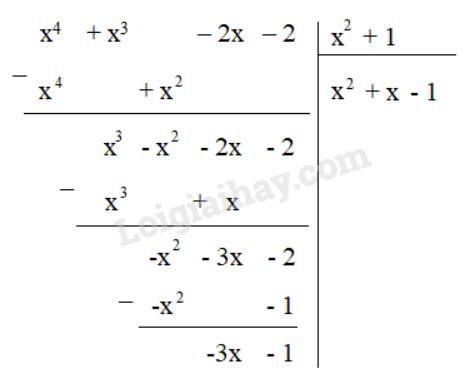
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
AH
Akai Haruma
Giáo viên
29 tháng 2 2024
Bài 1:
Do $ƯCLN(a,b)=16$ nên đặt $a=16x, b=16y$ với $x,y$ tự nhiên và $x,y$ nguyên tố cùng nhau.
Khi đó:
$a+b=96$
$\Rightarrow 16x+16y=96$
$\Rightarrow x+y=6$
Mà $x,y$ nguyên tố cùng nhau nên $(x,y)=(1,5), (5,1)$
$\Rightarrow (a,b)=(16,80), (80,16)$
AH
Akai Haruma
Giáo viên
29 tháng 2 2024
Bài 2:
Do $ƯCLN(a,b)=8\Rightarrow$ đặt $a=8x, b=8y$ với $x,y$ là số tự nhiên nguyên tố cùng nhau.
Khi đó:
$ab=8x.8y=384$
$\Rightarrow xy=6$
Do $x,y$ nguyên tố cùng nhau nên $(x,y)=(1,6), (2,3), (3,2), (6,1)$
$\Rightarrow (x,y)=(8,48), (16, 24), (24,16), (48,8)$
VQ
8 tháng 4 2020
Giải:
Ta có:
6a + 9 chia hết cho a - 1
=> 6a - 6 + 6 + 9 chia hết cho a - 1
=> 6(a-1) + 15 chia hết cho a-1
Ta thấy: 6(a-1) chia hết cho a-1
=> a-1 thuộc vào Ư(15)
=> a-1 = {+1;-1;+5;-5;+3;-3;+15;-15}
Ta có bảng sau:
| a-1 | 1 | -1 | 5 | -5 | 3 | -3 | 15 | -15 |
| a | 2 | 0 | 6 | -4 | 4 | -2 | 16 | -14 |
nếu đúng thì kết bn vs mình nhes^_^
chúc bn hok tốt
29 tháng 12 2021
a: \(\overrightarrow{MA}=\left(1-x_M;-1\right)\)
\(\overrightarrow{MB}=\left(3-x_M;0\right)\)
Để ΔMAB vuông tại M thì \(\left(1-x_M\right)\left(3-x_M\right)-1=0\)
=>xM=2