- x+1/2019+x+1/2020=x+1/2021
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2021
ĐKXĐ : \(\left\{{}\begin{matrix}x>2019\\y>2020\\z>2021\end{matrix}\right.\)
Đặt \(\sqrt{x-2019}=a,......\)
Ta được PT : \(\dfrac{1-a}{a^2}+\dfrac{1-b}{b^2}+\dfrac{1-c}{c^2}+\dfrac{3}{4}=0\)
\(\Leftrightarrow\dfrac{1}{a^2}-\dfrac{1}{a}+\dfrac{1}{4}+\dfrac{1}{b^2}-\dfrac{1}{b}+\dfrac{1}{4}+\dfrac{1}{c^2}-\dfrac{1}{c}+\dfrac{1}{4}=0\)
\(\Leftrightarrow\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{b}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{c}-\dfrac{1}{2}\right)^2=0\)
- Thấy : \(\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2\ge0,......\)
\(\Rightarrow\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{b}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{c}-\dfrac{1}{2}\right)^2\ge0\)
- Dấu " = " xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{2}\\\dfrac{1}{b}=\dfrac{1}{2}\\\dfrac{1}{c}=\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=2\\c=2\end{matrix}\right.\)
- Thay lại a. b. c ta được : \(\left\{{}\begin{matrix}\sqrt{x-2019}=2\\\sqrt{y-2020}=2\\\sqrt{z-2021}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2019=4\\y-2020=4\\z-2021=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2023\\y=2024\\z=2025\end{matrix}\right.\) ( TM )
Vậy ...
NA
0
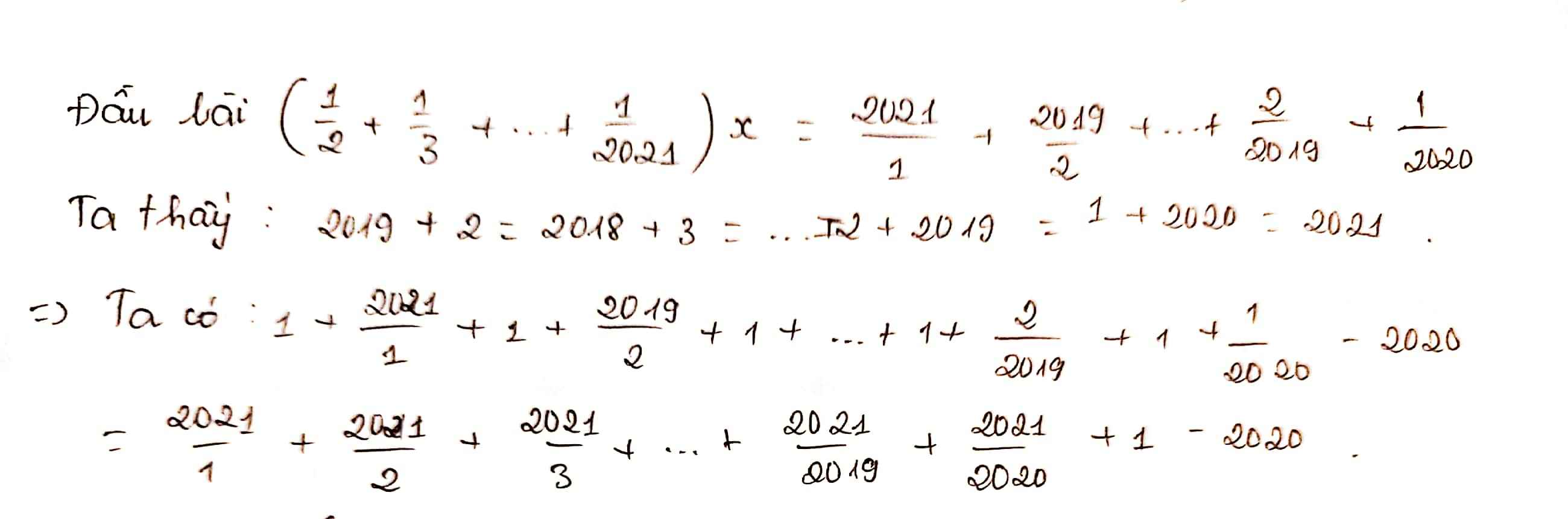
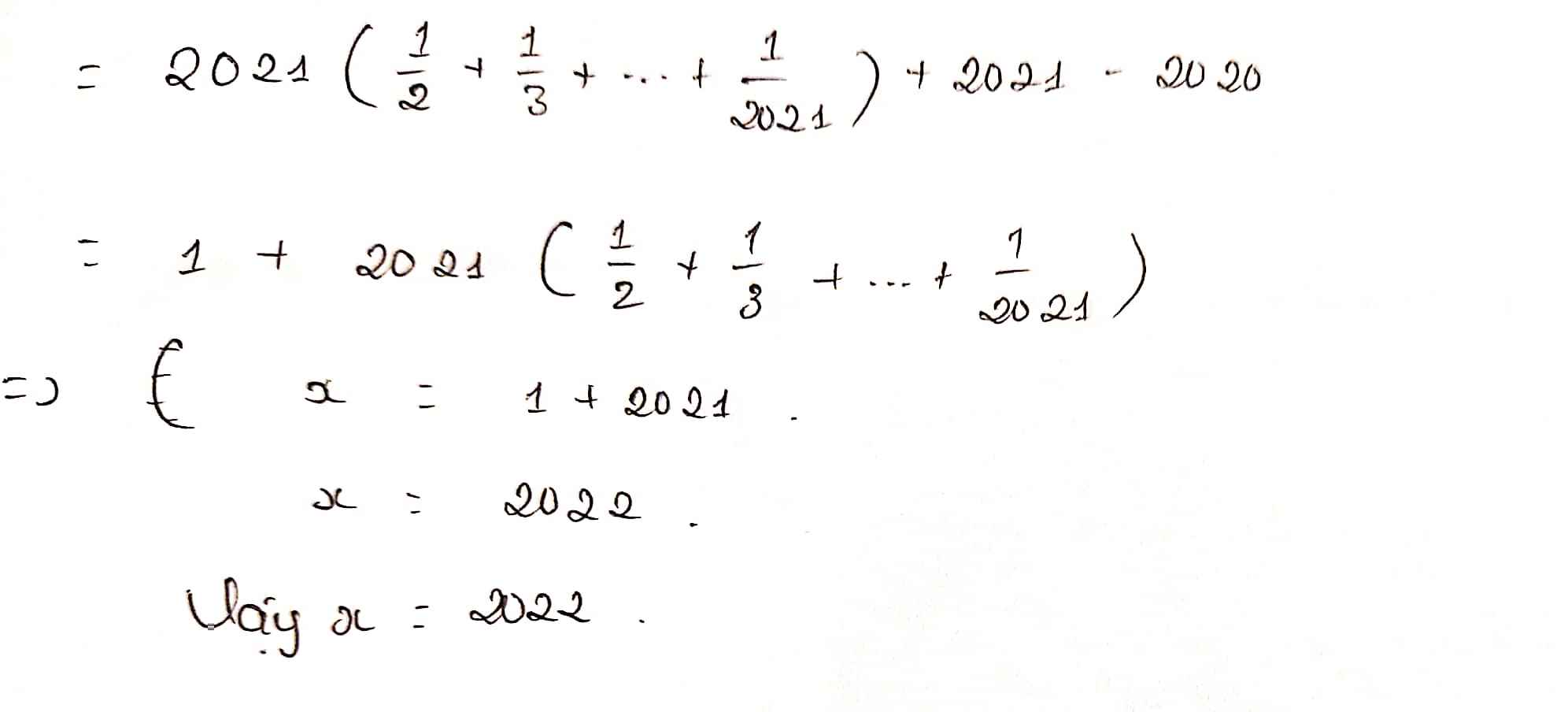
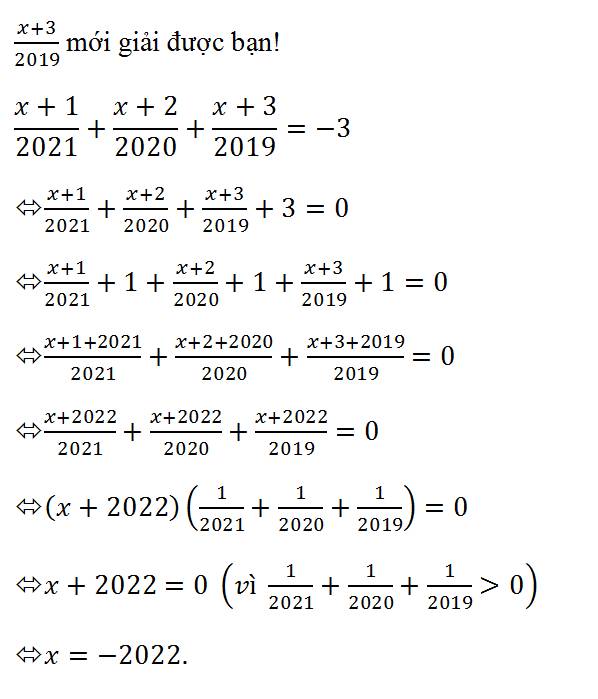
Ta có: \(\frac{x+1}{2019}+\frac{x+1}{2020}=\frac{x+1}{2021}\)
\(\Leftrightarrow\frac{x+1}{2019}+\frac{x+1}{2020}-\frac{x+1}{2021}=0\)
\(\Leftrightarrow\left(x+1\right)\left(\frac{1}{2019}+\frac{1}{2020}-\frac{1}{2021}\right)=0\)
Mà \(\frac{1}{2019}+\frac{1}{2020}-\frac{1}{2021}>0\)
\(\Rightarrow x+1=0\Rightarrow x=-1\)
\(\frac{x+1}{2019}+\frac{x+1}{2020}=\frac{x+1}{2021}\)
\(\frac{x+1}{2019}+\frac{x+1}{2020}-\frac{x+1}{2021}=0\)
\(\left(x+1\right)\left(\frac{1}{2019}+\frac{1}{2020}-\frac{1}{2021}\right)=0\)
\(x+1=0\left(\frac{1}{2019}+\frac{1}{2020}-\frac{1}{2021}\ne0\right)\)
\(x=0-1=-1\)