Tìm m để hàm số y= (m2 +1)x4 -2(m4+1)x2 +3-m có giá trị cực đại bằng 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 10 2018
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có 
R
Phương trình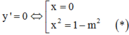 
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác 
Khi đó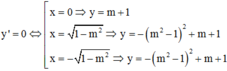 
Gọi 
; 
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là 
Và 
Diện tích tam giác ABC là 
Mà 
R suy ra 
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
CM
24 tháng 9 2019
Chọn C
[Phương pháp tự luận]
Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
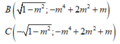
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
Vậy S đạt giá trị lớn nhất ⇔ m = 0
CM
15 tháng 3 2018
Ta có
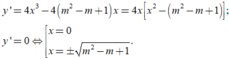
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó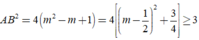 
Dấu xảy ra khi m=1/2.
Chọn B.
CM
11 tháng 1 2019
Chọn C.
Tập xác định: D = ℝ
Xét 
Với m = 1, hàm số đã cho trở thành: 
Hàm số này đạt cực tiểu tại điểm A(0;-1) nên không thỏa mãn yêu cầu bài toán.
Với m = -1, hàm số đã cho trở thành: 
Hàm số này đạt cực đại tại điểm B(0;-3) nên thỏa mãn yêu cầu bài toán.
Xét m
≠
±
1 ta có 
Xét y' = 0 
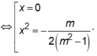
Với m = 0 phương trình y' = 0 có nghiệm bồi 3 và 
nên hàm số đạt cực đại tại điểm C(0;-1) nên thỏa mãn yêu cầu bào toán.
Với m ≠ 0 hàm số đã cho chỉ có một điểm cực đại và không có điểm cực tiểu khi và chỉ khi
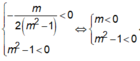
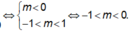
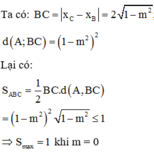
\(ab=-2\left(m^2+1\right)\left(m^4+1\right)< 0\) ;\(\forall m\)
\(\Rightarrow\) Hàm có 3 cực trị
Do hệ số \(a=m^2+1>0\) nên hàm trùng phương nhận \(x=0\) là cực đại
\(\Rightarrow y_{CĐ}=y\left(0\right)=3-m\)
\(\Rightarrow3-m=2\Rightarrow m=1\)
\(y'=\left(4m^2+4\right)x^3-\left(4m^4+4\right)x\)
\(y'=\left(4m^2+4\right)\left(x^3-x\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\\x=-1\end{matrix}\right.\)
\(y\left(\pm1\right)=-2m^4+m^2-m+2=0\Leftrightarrow m=0\)
\(y\left(0\right)=3-m=2\Leftrightarrow m=1\)