cho a.b=2 và a+b=5 .Tính a2+b2 và a3+b3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Rút gọn M = 279. Với m = 2017 giá trị của M = 279.
b) N = 8 a 3 - 27 b 3 = ( 2 a ) 3 - ( 3 b ) 3 = ( 2 a - 3 b ) 3 + 3.2a.3b.(2a - 3b)
Thay a.b = 12;2a - 3b = 5 ta thu được N - 1205.
c) Cách 1: Từ a + b = 1 Þ a = 1 - b thế vào K.
Thực hiện rút gọn K, ta có kết quả K = 1.
Cách 2: Tìm cách đưa biêu thức về dạng a + b.
a 3 + b 3 = ( a + b ) 3 – 3ab(a + b) = 1 - 3ab;
6 a 2 b 2 (a + b) = 6 a 2 b 2 kết hợp với 3ab( a 2 + b 2 ) bằng cách đặt 3ab làm nhân tử chung ta được 3ab( a 2 + 2ab + b 2 ) = 3ab.
Thực hiện rút gọn K = 1.

`a)a(2+b)+b(a+2)`
`=2a+ab+ab+2b`
`=2(a+b)+2ab`
`=2.10+2.(-36)`
`=20-72=-52`
`b)a^2+b^2`
`=(a+b)^2-2ab`
`=10^2-2.(-36)`
`=100+72=172`
`c)a^3+b^3`
`=(a+b)(a^2-ab+b^2)`
`=10[(a+b)^2-3ab]`
`=10[10^2-3.(-36)]`
`=10(100+108)`
`=10.208=2080`
a, \(=>2a+ab+ab+2b=2\left(a+b+ab\right)=2\left(10-36\right)=-52\)
b, \(a^2+b^2=a^2+2ab+b^2-2ab=\left(a+b\right)^2-2ab=\left(10\right)^2-2\left(-36\right)=172\)
c, \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=10\left[\left(a+b\right)^2-3ab\right]\)
\(=10\left[10^2-3\left(-36\right)\right]=2080\)

b) Ta có: \(a^2+b^2\)
\(=\left(a-b\right)^2+2ab\)
\(=3^2+2\cdot\left(-2\right)=9-4=5\)
c) Ta có: \(a^3-b^3\)
\(=\left(a-b\right)^3-3ab\left(a-b\right)\)
\(=3^3-3\cdot\left(-2\right)\cdot3\)
\(=27+18=45\)

Công thức tổng quát: n.(n-1).(n-2)/6 với n là số điêm đã cho.
Do A1,A2,A3,O thẳng hàng nên có 4 tam giác không tạo thành
Vậy theo bài ra: (7x6x5)/6-8= 27

VP `=(a+b)(a^2-ab+b^2)`
`=a^3-a^2b+ab^2+a^2b-ab^2+b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)+b^3`
`=a^3+b^3`
.
VP `=(a-b)(a^2+ab+b^2)`
`=a^3+a^2b+ab^2-a^2b-ab^2-b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)-b^3`
`=a^3-b^3`

Từ (1) và (2) suy ra: a 2 < b 2
Ta có: a < b ⇒ a 3 < a 2 b (3)
a < b ⇒ a b 2 < b 3 (4)
a < b ⇒ a.a.b < a.b.b ⇒ a 2 b < a b 2 (5)
Từ (3), (4) và (5) ⇒ a 3 < b 3

\(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
=1
\(M=\left(a^2+b^2+2-a^2-b^2+2\right)\left[\left(a^2+b^2+2\right)^2+\left(a^2+b^2+2\right)\left(a^2+b^2-2\right)+\left(a^2+b^2-2\right)^2\right]-12\left(a^2+b^2\right)^2\\ M=4\left(a^4+b^4+4+4a^2+4b^2+2a^2b^2+\left(a^2+b^2\right)^2-4+a^4+b^4+4-4a^2-4b^2+2a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2-3a^4-6a^2b^2-3b^4\right)\\ M=4\cdot4=164\)
CMR :1,a2+b2=<a+b>2-2ab
2,a3+b3=<a+b>3-3ab.<a+b>
3,a3-b3=<a-b>3+3ab.<a+b>
Cho :a+b=1
Tính :A=a3+b3+3ab

2
Ta có:
VP=(a+b)3−3ab(a+b)VP=(a+b)3-3ab(a+b)
=a3+b3+3ab(a+b)−3ab(a+b)=a3+b3+3ab(a+b)-3ab(a+b)
=a3+b3=VT(dpcm)
1, \(VT=a^2+b^2=a^2+b^2+2ab-2ab=\left(a+b\right)^2-2ab=VP\left(đpcm\right)\)
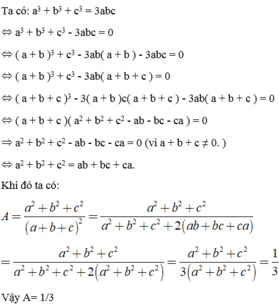
Lời giải:
Bạn vận dụng những hằng đẳng thức đáng nhớ thôi.
$a^2+b^2=a^2+2ab+b^2-2ab=(a+b)^2-2ab=5^2-2.2=21$
$a^3+b^3=(a+b)(a^2-ab+b^2)=(a+b)(a^2+b^2-ab)$
$=5(21-2)=5.19=95$