cho \(d:x-3y+5=0\)
Tìm d' là ảnh của d qua phép quay \(Q\left(0;60^o\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 9 2019
Đáp án B
Phương trình đường thẳng d đi qua A ( -2; 0) có dạng: A(x+ 2) + By= 0.
Theo giả thiết, ta có:
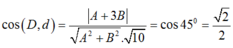
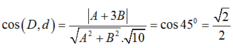
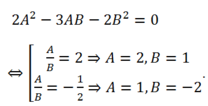
Vậy: d: 2x+ y+ 4= 0 hoặc d: x- 2y + 2= 0.
CM
17 tháng 11 2018
Chọn A
Phương trình tham số của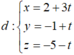 
Ta có M = d ∩ (P) nên 2 (2+3t)-3 (-1+t)-5-t-6=0 ó t = 2 => M (8 ; 1 ; -7)
VTCP của Δ là 
Δ đi qua M có VTCP 
nên có phương trình: 
CM
3 tháng 11 2019
Gọi là mặt phẳng chứa đường thẳng d và vuông góc với có vectơ pháp tuyến
Chọn C
HT
19 tháng 9 2020
Phép uay ua tâm O?
Phương pháp để làm dạng này, lấy \(K\left(x_1;y_1\right),I\left(x_2;y_2\right)\in\left(d\right)\) =>\(K'\left(x_1';y_1'\right);I'\left(x_2';y_2'\right)\) là ảnh của K' qua phép quay tâm O góc uay alpha. Khi đó \(K',I'\in\left(d'\right)\)
Áp dụng biểu thức tọa độ:
\(\left\{{}\begin{matrix}x_1'=x_1\cos\alpha-y_1\sin\alpha\\y_1'=x_1\sin\alpha+y_1\cos\alpha\end{matrix}\right.\)
Giờ ta sẽ áp dụng vô bài
Lấy \(K\left(1;2\right)\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}x_K'=1.\cos60^0-2.\sin60^0=\frac{\sqrt{3}}{2}-1\\y_K'=1.\sin60^0+2.\cos60=\frac{1}{2}+\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow K'\left(\frac{\sqrt{3}}{2}-1;\frac{1}{2}+\sqrt{3}\right)\)
\(I\left(4;3\right)\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}x_I'=4.\cos60^0-3\sin60^0=2\sqrt{3}-\frac{3}{2}\\y_I'=4\sin60^0+3\cos60^0=2+\frac{3\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow I'\left(2\sqrt{3}-\frac{3}{2};2+\frac{3\sqrt{3}}{2}\right)\)
Bạn tự làm nốt nha, giờ chỉ cần viết phương trình đt (d') đi ua 2 điểm K' và I' thôi. Cách chứng minh công thức kia tui chưa biết chứng minh, bởi tui mới đọc sơ sơ dạng này :( Để bao giờ tìm hiểu thêm
Nguyễn Việt Lâm: Giup mk vs bn.. :]]