nêu đường thẳng song song
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dấu hiệu:Nếu 1 đường thẳng cắt 2 đường thẳng và trong đó có 1 cặp góc so le trong bằng nhau(đồng vị bằng nhau),trong cùng phía bù nhau thì 2 đường thẳng đó song song với nhau
Tính chất:Nếu 1 đường thẳng cắt 2 đường thẳng song song thì:
-Hai góc trong cùng phía bù nhau
-Hai góc đồng vị bằng nhau:
-Hai góc so le trong bằng nhau
Tiêu đề Ơ-clit:Chỉ có 1 và chỉ 1 đường thẳng đi qua điểm M và song song với đường thẳng cho trước
Dấu hiệu nhận biết hai đường thẳng song song:
Nếu một đường thẳng cắt hai đường thẳng song song thì
+ Tạo thành hai góc so le trong bằng nhau
+ Tạo thành hai góc đồng vị bằng nhau
+ Tạo thành hai góc trong cùng phía bù nhau
Tính chất của hai đường thẳng song song:
Nếu một đường thẳng cắt hai đường thẳng song song thì
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Phát biểu tiên đề Ơclit:
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó .

Câu 1:
Hai góc đối đỉnh là hai góc có chung đỉnh, và hai tia của góc này là hai tia đối của hai tia của góc kia
Tính chất: Hai góc đối đỉnh thì bằng nhau
Câu 1 :- định nghĩa : 2 góc đối đỉnh là 2 góc mà là mỗi cạnh của góc này là tia đối của một cạnh của góc kia
- tính chất : 2 góc đối đỉnh thì bằng nha

Sử dụng êke
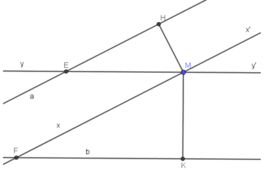
* Để vẽ đường thẳng xx’ đi qua M và song song với a, ta chỉ cần vẽ đường thẳng vuông góc với MH.
Thật vậy vì xx’ ⏊ MH, MH ⏊ a ⇒ xx’ // a.
Cách vẽ:
Đặt ê ke sao cho đỉnh góc vuông trùng với điểm M, một cạnh góc vuông trùng với MH.
Vẽ đoạn thẳng trùng với cạnh góc vuông còn lại của eke.
Kéo dài đoạn thẳng ta được đường thẳng xx’ cần vẽ.
* Tương tự với đường thẳng yy’

`a, AB` không song song `CD`
`b, EG` song song `HI`
`c, MN` không song song `PQ`
`d, ST` song song `XY`

hứng minh đường thẳng song song với đường thẳng:
Để chứng minh hai đường thẳng song song, ta sử dụng các định lí.
- Ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song với nhau.
- Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa d và cắt (α) theo giao tuyến d’ thì d’ song song với d.
- Hai mặt phẳng phân biệt cùng song song với với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Một mặt phẳng cắt hai mặt phẳng song song cho hai giao tuyến song song.
- Sử dụng các phương pháp của hình học phẳng. Tính chất đường trung bình, định lí Ta-lét đảo, cạnh đối hình bình hành…
- Sử dụng tính chất về cạnh bên, cạnh đáy của hình lăng trụ.

1. Nêu định nghĩa 2 đường thẳng song song
=> - Hai đường thẳng song song là hai đường thẳng không có điểm chung.
Kí hiệu a // b
- Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.
2. Dấu hiệu nhận biết 2 đường thẳng song song
Nếu đường thẳng c cắt hai đường thẳng a , b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì a và b song song với nhau.
Cre: mạng
Học tốt ạ;-;
1 dấu hiệu nhận bt đường thg song song là
+) cs cặp góc so le trong bằng nhau
+) cs cặp góc đồng vị bằng nhau
+) cs cặp góc cx phía trong kề bù

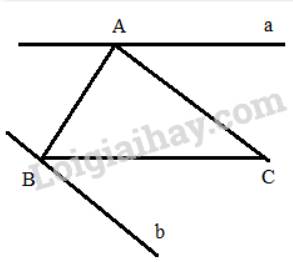
Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.
Ta được đường thẳng a đi qua A và song song với BC
Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.
Ta được đường thẳng b đi qua B và song song với AC
b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó
TL
Trong hình học Ơ cờ lít, hai đường thẳng được gọi là song song khi chúng cùng nằm trên một mặt phẳng và không có điểm chung. Trong trường hợp này, chúng được gọi là không cắt nhau, không giao nhau, hoặc không tiếp xúc nhau.
HT