\(\text{|x + 4| = |2x - 1}|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2023
a: TH1: x<-1/2
PT sẽ là -2x-1+3-x=4
=>-3x+2=4
=>-3x=2
=>x=-2/3(nhận)
TH2: -1/2<=x<3
Pt sẽ là 2x+1+3-x=4
=>x+4=4
=>x=0(nhận)
TH3: x>=3
=>x-3+2x+1=4
=>3x-2=4
=>x=2(loại)
b: TH1: x<-3/2
Pt sẽ là -2x-3+3-4x=x
=>-6x=x
=>x=0(loại)
TH2: -3/2<=x<3/4
PT sẽ là 2x+3+3-4x=x
=>-2x+6-x=0
=>-3x=-6
=>x=2(loại)
TH3: x>=3/4
PT sẽ là 2x+3+4x-3=x
=>6x=x
=>x=0(loại)
12 tháng 5 2021
\(\dfrac{4-x}{-5}=\dfrac{-5}{4-x}\)
\(\left(4-x\right)^2=25=5^2=\left(-5\right)^2\)
4-x=5 hoặc 4-x=-5
x=-1 hoặc x=9
22 tháng 10 2021
\(a,\Leftrightarrow2x^3-x^2+ax+b=\left(x-1\right)\left(x+1\right)\cdot a\left(x\right)\)
Thay \(x=1\Leftrightarrow2-1+a+b=0\Leftrightarrow a+b=-1\)
Thay \(x=-1\Leftrightarrow-2-1-a+b=0\Leftrightarrow b-a=3\)
Từ đó ta được \(\left\{{}\begin{matrix}a+b=-1\\-a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)
\(b,\Leftrightarrow ax^3+bx^2+2x-1=\left(x-1\right)\left(x+6\right)\cdot b\left(x\right)\)
Thay \(x=1\Leftrightarrow a+b+2-1=0\Leftrightarrow a+b=-1\)
Thay \(x=-6\Leftrightarrow-216a+36b+12-1=0\Leftrightarrow216a-36b=11\)
Từ đó ta được \(\left\{{}\begin{matrix}a+b=-1\\216a-36b=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{25}{252}\\b=-\dfrac{227}{252}\end{matrix}\right.\)
\(c,\Leftrightarrow ax^4+bx^3+1=\left(x+1\right)^2\cdot c\left(x\right)\)
Thay \(x=-1\Leftrightarrow a-b+1=0\Leftrightarrow b=a+1\)
\(\Leftrightarrow ax^4+\left(a+1\right)x^3+1⋮\left(x+1\right)\\ \Leftrightarrow ax^4+ax^3+x^3+1⋮\left(x+1\right)\\ \Leftrightarrow ax^3\left(x+1\right)+\left(x+1\right)\left(x^2-x+1\right)⋮\left(x+1\right)\\ \Leftrightarrow\left(x+1\right)\left(ax^3+x^2-x+1\right)⋮\left(x+1\right)\\ \Leftrightarrow ax^3+x^2-x+1⋮\left(x+1\right)\)
Thay \(x=-1\Leftrightarrow-a+1+1+1=0\Leftrightarrow a=3\Leftrightarrow b=4\)
27 tháng 1 2023
=>1/2x-3/4y-1/5x-1/5y+1/5=2x-y-1 và 4(x+y-1)+3(4x-y-2)=2(2x-y-3)
=>-17/10x+1/20y=-6/5 và \(4x+4y-4+12x-3y-6=4x-2y-6\)
=>-17/10x+1/20y=-6/5 và 12x+3y=4
=>x=2/3; y=-4/3
8 tháng 3 2022
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
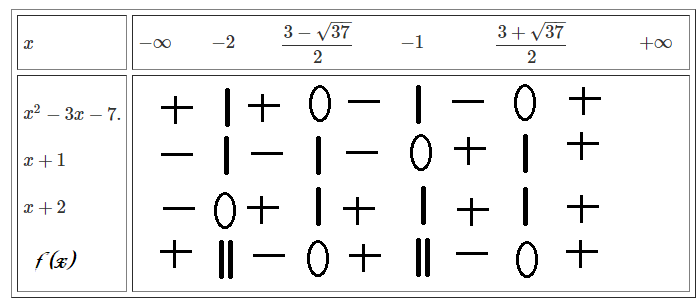
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
1 tháng 12 2021
\(a,\left(12x^2y^2-6xy^2\right):3xy+2y=6xy^2\left(2x-1\right):3xy+2y=2y\left(2x-1\right)+2y=4xy-2y+2y=4xy\)
\(b,\dfrac{4}{x+1} + \dfrac{8}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{4\left(x-1\right)+8}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{4x-4+8}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{4x+4}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{4\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4}{x-1}\)
\(c,\dfrac{1 }{x+1}- \dfrac{1}{x-1} +\dfrac{ 2x}{x^2-1} \)
\(=\dfrac{x-1}{\left(x+1\right)\left(x-1\right)}-\dfrac{x+1}{\left(x+1\right)\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x-1-x-1+2x}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{2x-2}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{2}{x+1}\)
1 tháng 12 2021
\(a,=4xy-2y+2y=4xy\\ b,\dfrac{4}{x+1}+\dfrac{8}{\left(x+1\right)\left(x-1\right)}=\dfrac{4x-4+8}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{4x+4}{\left(x+1\right)\left(x-1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\\ c,\dfrac{1}{x+1}-\dfrac{1}{x-1}+\dfrac{2x}{x^2-1}=\dfrac{x-1-x-1+2x}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{2x-2}{\left(x-1\right)\left(x+1\right)}=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{2}{x+1}\)
Bài làm:
Ta có: \(\left|x+4\right|=\left|2x-1\right|\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=2x-1\\x+4=1-2x\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=5\\3x=-3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)
ok tks