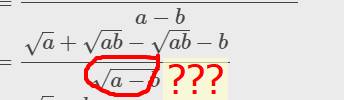Rút gọn:
a + b + \(\sqrt b + \sqrt{a + b} \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TK
0
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2024
Biểu thức này có thể coi là ko rút gọn được, thứ duy nhất rút gọn được là ở phân thức đằng sau, \(\dfrac{a\sqrt[]{b}-b\sqrt[]{a}}{\sqrt[]{ab}}=\sqrt[]{a}-\sqrt[]{b}\)
Ngoài ra thì hết rồi, vẫn rất cồng kềnh
8 tháng 10 2021
\(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}-\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}-\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}\)
\(=\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}=0\)
8 tháng 10 2021
Đk: \(a,b\ge0\) và \(a\ne b\)
\(\dfrac{a+b-\sqrt{2ab}}{\sqrt{a}-\sqrt{b}}-\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}-\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}\)
\(=\sqrt{a}-\sqrt{b}-\left(\sqrt{a}-\sqrt{b}\right)=0\)
H9
HT.Phong (9A5)
CTVHS
7 tháng 11 2023
\(\dfrac{\sqrt{a}+\sqrt{ab}}{a-b}-\dfrac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}\left(a,b\ge0;a\ne b\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{ab}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{\sqrt{a}+\sqrt{ab}-\sqrt{ab}-b}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{\sqrt{a}-b}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{\sqrt{a}-b}{a-b}\)
26 tháng 5 2022
\(B=\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}.\sqrt{b}}\)
\(B=\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}.\sqrt{ab}\)
\(B=a\sqrt{b}-b\sqrt{a}\)
30 tháng 1 2024
\(A=\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{1}{a-b}\left(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\right)\)
\(=\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{1}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\left(\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\right)\)
\(=\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{a+2\sqrt{ab}+b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{2\sqrt{b}-\sqrt{a}-\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{-\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)
=-1
26 tháng 12 2021
\(=\dfrac{a+2\sqrt{ab}+b-a+2\sqrt{ab}-b}{a-b}\cdot\dfrac{\sqrt{ab}\cdot\sqrt{a-b}}{ab}\)
\(=\dfrac{4ab}{ab}\cdot\dfrac{1}{\sqrt{a-b}}=\dfrac{4}{\sqrt{a-b}}\)
AM
26 tháng 12 2021
=\(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)
=\(\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}-\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)
=\(0\)
17 tháng 9 2021
\(\dfrac{a\sqrt{a}+b\sqrt{b}}{2\sqrt{a}+2\sqrt{b}}=\dfrac{a-\sqrt{ab}+b}{2}\)
17 tháng 9 2021
\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{2\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{a+\sqrt{ab}+b}{2}\)
6 tháng 12 2023
\(P=\left(\dfrac{\sqrt{a}-b}{\sqrt{a}+b}-\dfrac{\sqrt{a}+b}{\sqrt{a}-b}\right)\cdot\left(\sqrt{a^3}-\dfrac{ab^2}{\sqrt{a}}\right)\)
\(=\dfrac{\left(\sqrt{a}-b\right)^2-\left(\sqrt{a}+b\right)^2}{\left(\sqrt{a}+b\right)\left(\sqrt{a}-b\right)}\cdot\dfrac{\sqrt{a^4}-ab^2}{\sqrt{a}}\)
\(=\dfrac{\left(\sqrt{a}-b-b-\sqrt{a}\right)\left(\sqrt{a}-b+b+\sqrt{a}\right)}{\left(\sqrt{a}+b\right)\left(\sqrt{a}-b\right)}\cdot\dfrac{a^2-ab^2}{\sqrt{a}}\)
\(=\dfrac{\left(-2b\right)\cdot\left(2\sqrt{a}\right)}{a-b^2}\cdot\dfrac{a\left(a-b^2\right)}{\sqrt{a}}\)
\(=\dfrac{-4b\sqrt{a}}{\sqrt{a}}\cdot a=-4ba\)