B=22005 - 22004 - 22003 - ... - 2 - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
H9
HT.Phong (9A5)
CTVHS
13 tháng 11 2023
Ta có:
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+....+2^{2002}\right)\)
\(A=2^{2003}-1\)
Mà: \(2^{2003}=2^{2003}\)
\(\Rightarrow2^{2003}-1< 2^{2003}\)
\(\Rightarrow A< B\)
LH
14 tháng 10 2023
mik bt lm câu 1 thôi nha, bn thông cảm:
a = 2007.2009 b = 20082
=(2008 - 1)(2008 + 1)
= 20082 - 1
Ta có, a = 20082 - 1, b = 20082
mà 20082 - 1 < 20082
=> a < b
NA
Nguyễn An Ninh
VIP
14 tháng 5 2023
\(S=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2005}}\)
\(2.S=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(2.S-S=\left(2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(S=2-\dfrac{1}{2^{2006}}\)
TP
2
13 tháng 10 2024
A = 2 + 22 + 23 + … + 22004 . Chứng minh rằng A chia hết cho 3 , cho 7.
10 tháng 8 2021
\(2^{2004}=\left(2^{668}\right)^3\)
\(5^{891}=\left(5^{297}\right)^3\)
mà \(2^{668}>5^{297}\)
nên \(2^{2004}>5^{891}\)
NN
0
QL
19 tháng 8 2021
Đặt A=22+23+..+22005
2A=23+24+..+22006
suy ra 2A-A=(23+24+..+22006) - (22+23+..+22005)
A=22006-22
suy ra C=4+22006-4
C=22006 .Là lũy thừa của 2 (đpcm)
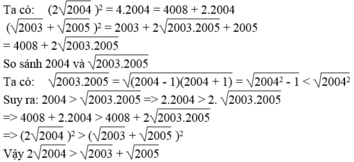
\(B=2^{2005}-2^{2004}-2^{2003}-...-2-1\)
\(B=2^{2005}-\left(2^{2004}+2^{2003}+...+2+1\right)\)
Đặt \(A=1+2+...+2^{2004}\) \(\Rightarrow2A=2+2^2+...+2^{2005}\)
\(2A-A=\left(2+2^2+...+2^{2005}\right)-\left(1+2+...+2^{2004}\right)\)
\(A=2^{2005}-1\). Thay A vào B, ta có :
\(B=2^{2005}-\left(2^{2005}-1\right)=2^{2005}-2^{2005}+1=1\)
Ta có : B = 22005 - 22004 - 22003 - ... - 2 - 1
= B = 22005 - (22004 + 22003 + ... + 2 + 1)
Đặt A = 22004 + 22003 + ... + 2 + 1
=> 2A = 22005 + 22004 + .... + 22 + 2
Lấy 2A trừ A theo vế ta có
2A - A = (22005 + 22004 + .... + 22 + 2) - (22004 + 22003 + ... + 2 + 1)
A = 22005 - 1
Khi đó B = 22005 - (22005 - 1) = 1