Tìm m để y = mx3 - x2 + 3x + m - 2 đồng biến trên (-3,0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 7 2019
Đáp án A
TXĐ: D= ℝ
y = m x 3 - x 2 + 2 x + m - 1
⇒ y ' = 3 m x 2 - 2 x + 2
Để y = m x 3 - x 2 + 2 x + m - 1 đồn biến trên khoảng - 2 ; 0 thì
y ' = 3 m x 2 - 2 x + 2 > 0 ∀ x ∈ - 2 ; 0
hay 2 x - 2 3 x 2 < m ∀ x ∈ - 2 ; 0
xét f x = 2 x - 2 3 x 2 có
f ' x = 2 . 3 x 2 - 6 x 2 x - 2 9 x 4 = - 6 x 2 + 12 x 9 x 4 = 0
⇔ x=0 hoặc x=2
Ta có bảng biến thiên
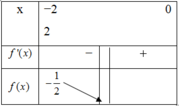
vậy f x = 2 x - 2 3 x 2 < m ∀ x ∈ - 2 ; 0 ⇔ m > - 1 2
CM
28 tháng 2 2019
Đáp án B
Xét m = 0 ta có y = x +2 là hàm đồng biến nên m = 0 thỏa mãn
Hàm số nghịch biến trên R 
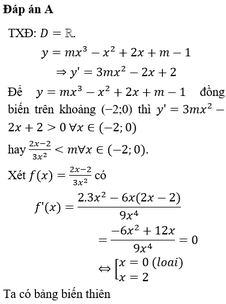
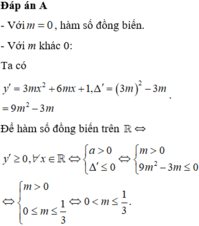
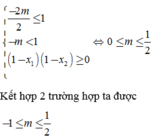
- Với \(m=0\) thỏa mãn
- Với \(m\ne0\Rightarrow y'=f\left(x\right)=3mx^2-2x+3\)
Để hàm số đồng biến trên \(\left(-3;0\right)\Leftrightarrow f\left(x\right)\ge0\) ; \(\forall x\in\left(-3;0\right)\)
\(\Leftrightarrow3mx^2-2x+3\ge0\Leftrightarrow3m\ge\frac{2x-3}{x^2}\)
\(\Leftrightarrow3m\ge\max\limits_{\left(-3;0\right)}\frac{2x-3}{x^2}\)
Xét \(g\left(x\right)=\frac{2x-3}{x^2}\Rightarrow g'\left(x\right)=\frac{6-2x}{x^3}< 0\) ; \(\forall x\in\left(-3;0\right)\)
\(\Rightarrow g\left(x\right)\) nghịch biến \(\Rightarrow g\left(x\right)< g\left(-3\right)=-1\)
\(\Rightarrow3m\ge-1\Leftrightarrow m\ge-\frac{1}{3}\)