cmr : Với k là stn thì \(25^k+1⋮25+1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
0
JN
1
T
7 tháng 1 2020
Áp dụng nguyên lý Di-rich-le, ta có:
Gọi các số: 3, 32, ..., 31001. Theo nguyên lý Di-rich-le luôn luôn tồn tại 2 số trong 1001 số trên khi chia cho 1000 có cùng số dư.
Giả sử 2 số: 3m và 3n trong đó \(1\le n\le m\le1001\)
\(\Rightarrow3^m-3^n⋮1000\)
\(\Rightarrow3^n.\left(3^{m-n}-1\right)⋮1000\)
Vì 3n không chia hết cho 1000 nên => \(3^{m-n}-1⋮1000\)
\(\Rightarrow3^{m-n}-1=100k\left(k\in N\right)\)
\(\Rightarrow3^{m-n}=1000k+1\)
\(\Rightarrow3^{m-n}\)có tận cùng là \(001\left(đpcm\right)\)
TP
1
21 tháng 12 2018
co:n^2+n+1
=n.n+n+1
=n.[n+1]+1
co:n.[n+1]la h cua 2 so tu nhien lien tiep
ma h cua 2 so tu nhien lien tiep luon la 1so chan
=>n.[n+1]+1 la so le
=>n.[n+1]+1 ko chia het cho 2 hay n^2+n+1 ko chia het cho 2
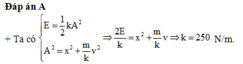
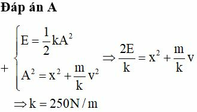
Đề thiếu với \(k=2n+1\) ( số lẻ )
Ta luôn có HĐT : \(x^{2n+1}+1^{2n+1}\)
\(=x^{2n+1}+1=\left(x+1\right)\left(x^{2n}-x^{2n-1}+x^{2n-2}-....+1\right)\)
Do đó : \(x^{2n+1}+1⋮x+1\)
Áp dụng vào bài toán thì : \(25^k+1⋮25+1\) với k lẻ.
Bạn thử k = 2 thì đâu có được, sửa đề: CMR: 25k - 1 \(⋮\)25 - 1
Bg
Ta có: 25k - 1 (k \(\inℕ\))
=> 25k - 1 = 25k - 25k - 1 + 25k - 1 - 25k - 2 + 25k - 2 - 25k - 3 +...+ 25 - 1
=> 25k - 1 = (25k - 25k - 1) + (25k - 1 - 25k - 2) + (25k - 2 - 25k - 3) +...+ (25 - 1)
=> 25k - 1 = (25k - 1.25 - 25k - 1) + (25k - 2.25 - 25k - 2) + (25k - 3.25 - 25k - 3) +...+ 1.(25 - 1)
=> 25k - 1 = [25k - 1.(25 - 1)] + [25k - 2.(25 - 1)] + [25k - 3.(25 - 1)] +...+ 1.(25 - 1)
=> 25k - 1 = (25 - 1)(25k - 1 + 25k - 2 + 25k - 3 +...+ 1) \(⋮\)25 - 1
=> 25k - 1 \(⋮\)25 - 1
=> ĐPCM